B站视频地址:【喵星考拉】傅里叶变换究极入门课程_哔哩哔哩_bilibili
线性代数相关:坐标变换
坐标变换公式:
注:视频中这里的公式有误
首先,第一行$\mathbf{u_i}$表示一个列向量,不用转置;
其次,第二行$u_{j,k}$的计算式不应该对$k$求和,应该对两个向量的每个分量相乘求和
含义:
系$i$下的坐标=系$j$下各正交基的线性组合
系$j$下各正交基的系数=系$i$下的坐标$\cdot$系$j$中各正交基在系$i$下的坐标(投影)
写成矩阵($\mathbf{V_{i,j}}$是$\mathbf{v_{i,j,k}}$按列拼起来的矩阵):
取转置(正交矩阵的转置为其逆):
无穷维向量——函数
把函数理解为无穷维向量
向量内积:
函数内积:
函数的坐标变换——积分变换
上式中,$\left\langle f(x),g(x) \right\rangle$是一个数,相当于是一个坐标值;
由于函数是无穷维向量,想复原这个无穷维向量,需要无穷个坐标值。
因此有:
其中$F(\omega)$称为“像函数”,相当于“新坐标系下无穷个坐标值”;$g(x,\omega)$是“无穷个正交函数组”,此之谓“积分变换”!
可以用像函数复原原函数:
复数、复变函数的内积
需要取共轭(否则不满足$\left\langle \mathbf{a,a} \right\rangle=||a||^2$)
复空间中的积分变换
正变换:
逆变换:
注意,正变换要取共轭(相当于求内积/坐标值);逆变换不取共轭(相当于基函数的线性组合)
工程学理论——微分方程
弹簧-质量-阻尼 力学系统:
电容-电阻-电感 电学系统:
二阶常系数微分方程求解:怎么解?
差分与微分,求和与积分
可用矩阵计算差分:

可用矩阵计算求和:

函数的求导看作无穷维矩阵:
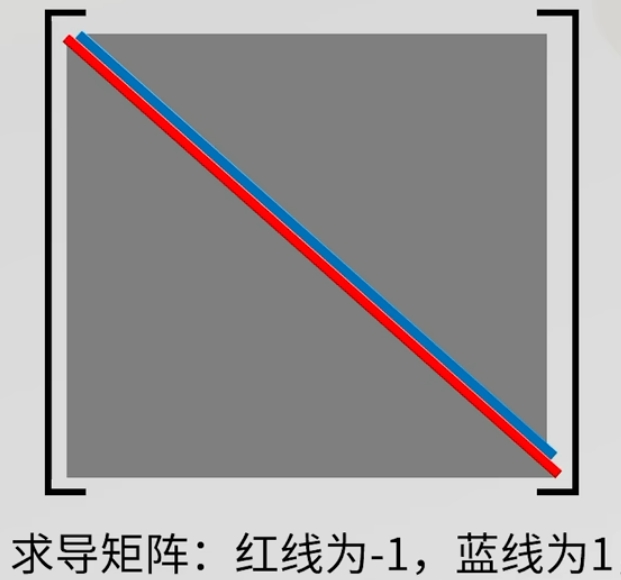
函数的积分看作无穷维矩阵:

求导、积分矩阵的“特征向量”
指数函数!
令$s=\sigma+j\omega$,得到三角函数
指数函数与三角函数的关系
注意到,两个复指数项的系数是共轭的
特征向量的用处
由于求导/积分运算的特征函数是复指数,因此若能把一个函数表示成复指数的线性组合,就能把微分方程化为代数方程
用特征函数解微分方程
略(注意有重根时的推导)
用三角函数作为正交基
定理:周期函数可以表示为具有相同周期的复指数函数的线性组合,这些函数两两正交且归一(证明略)
周期函数的频率分解——傅里叶级数
设有一个周期函数$f(t)$周期为$T$,即频率$f_0=\frac{1}{T}$,角频率$\omega_0=2\pi f_0$,希望找到它在各个复指数基函数($f_0,2f_0,3f_0,\dots,nf_0,\dots$)上的投影(求投影):
由投影复原原函数(求线性组合):
频率间隔:$\Delta f=f_0=\frac{1}{T}$,故周期越长,频谱越密,最终趋于连续函数
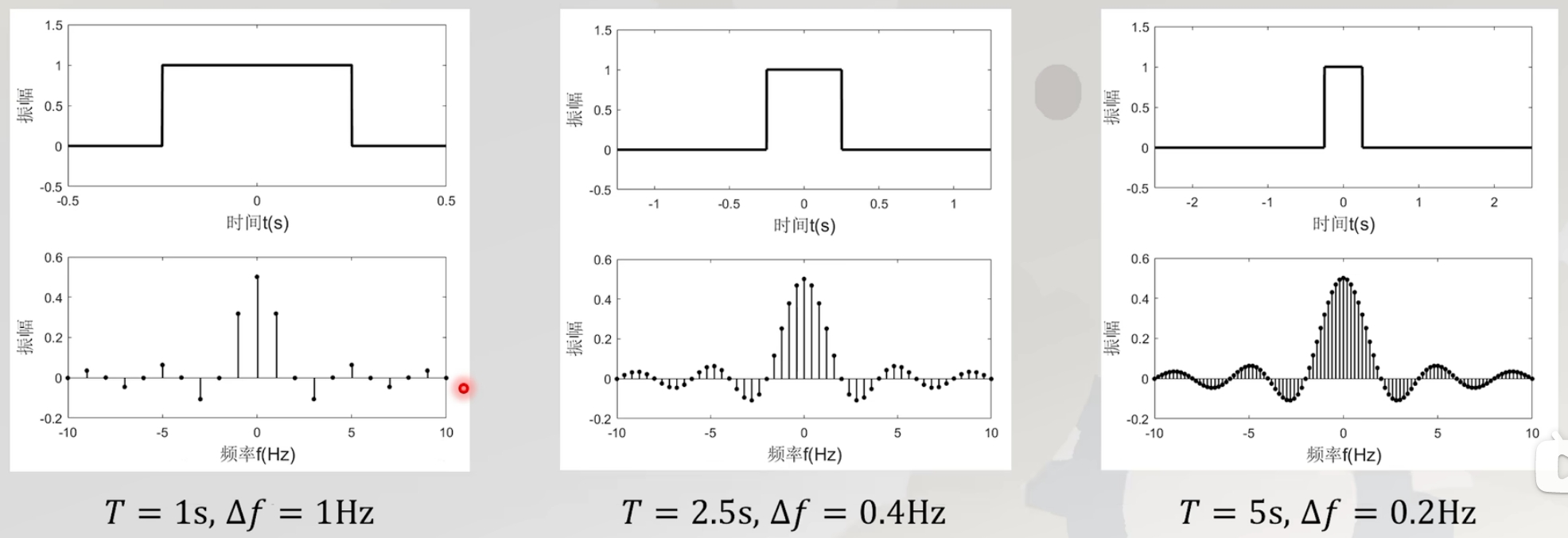
非周期函数的频率分解——傅里叶变换
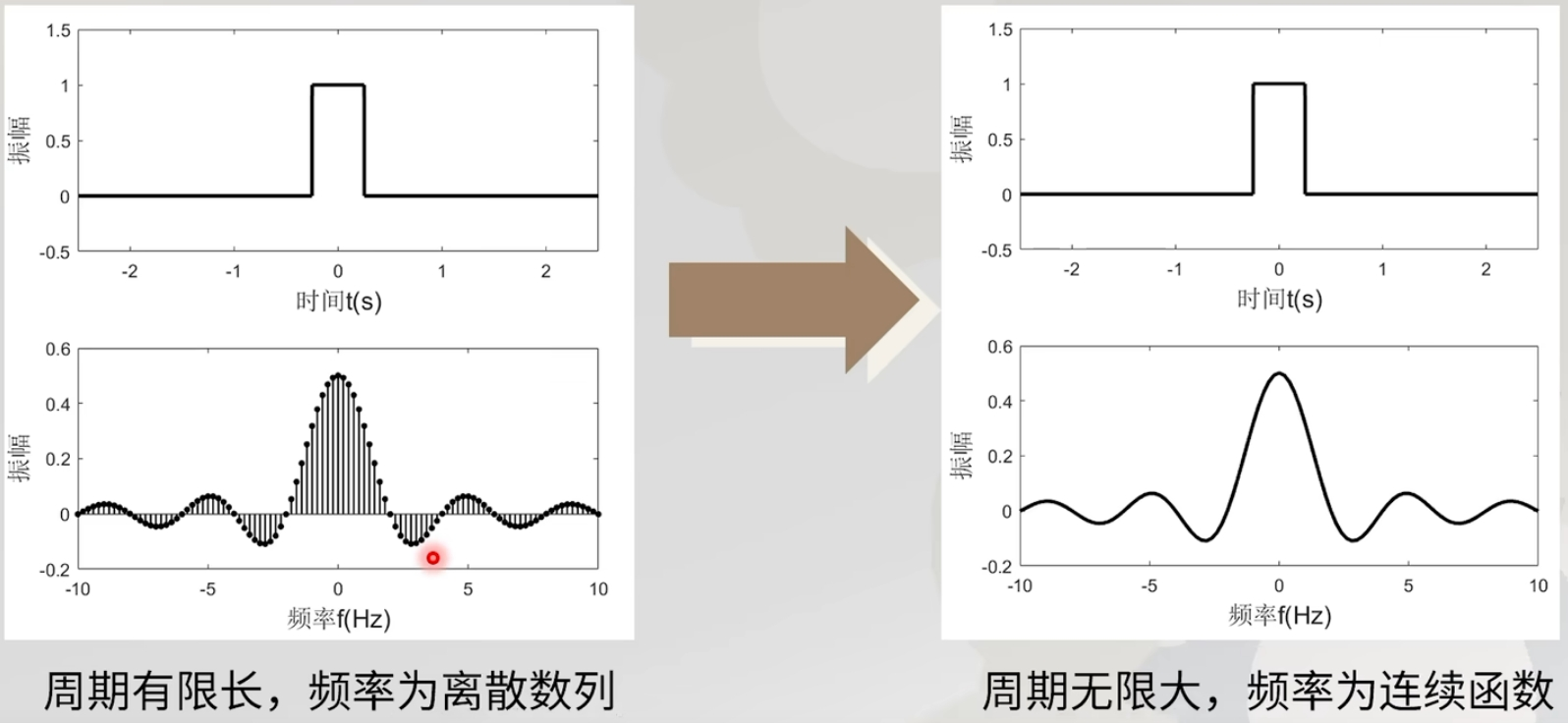
正变换(求投影):
逆变换(求线性组合):
