复变函数与积分变换

复数及其表示

复数的概念及代数运算

$z=x+iy$
和、差、积、商

复数的几何表示

复平面、模
用平行四边形法则求复数的和差
三角不等式
幅角、幅角主值
三角表示：$z=r(\cos\theta+i\sin\theta)$
指数表示：$z=re^{i\theta}$
乘积：模相乘、幅角相加

幂与根

$n$次幂：$z^n=r^n(\cos n\theta+i\sin n\theta)$
棣莫弗公式：当$r=1$时，有：$(\cos\theta+i\sin\theta)^n=\cos n\theta+i\sin n\theta$
$n$次方根：

• $\sqrt[n]{z}=r^{\frac{1}{n}}(\cos\frac{\theta+2k\pi}{n}+i\sin\frac{\theta+2k\pi}{n}), \ k=0,1,2,\dots,n-1$
• 几何上，是以原点为中心，$r^{\frac{1}{n}}$为半径的圆内接正$n$边形的$n$个顶点

注意

复数不能比较大小

平面概念及复球面

复平面上的曲线与区域

邻域、去心邻域、内点、开集、聚点、闭集、有界/无界点集、区域、有界/无界区域、边界点、边界

连续曲线：由复数方程$z=z(t)=x(t)+iy(t),\ a\le t\le b$所确定的平面点集称为复平面上的连续曲线，其中$x(t)$和$y(t)$是两个连续的实变函数

光滑曲线：在$a\le t\le b$上，$x^{\prime}(t)$和$y^{\prime}(t)$都是连续的，且对每个$t$都有$[x^{\prime}(t)]^2+[y^{\prime}(t)]^2\ne0$

简单曲线/若尔当曲线：没有重点的曲线
简单闭曲线：起点和终点重合的简单曲线

单连通域：复平面上的一个区域$B$，若在其中任作一条简单闭曲线，曲线的内部总属于$B$
多连通域：反之

复球面

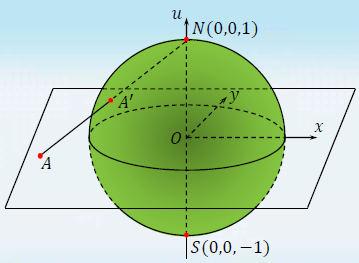
$A(x,y,0)$ 在复平面上，$A^{\prime}(x_1,y_1,z_1)$在复球面上

$$x_1=\frac{z+\bar{z}}{|z|^2+1},\ y_1=\frac{z-\bar{z}}{(|z|^2+1)i},\ z_1=\frac{|z|^2-1}{|z|^2+1}$$ $$z=x+iy=\frac{x_1+iy_1}{1-z_1}$$

球面上每一个点都有唯一的复数与之对应，北极$N$对应$\infty$
复数$\infty$的实部、虚部、辐角等概念无意义，模无穷大

扩充复平面：包括无穷远点的复平面
有限复平面：不包括无穷远点的复平面

解析函数

复变函数的概念

复变函数：存在一个确定的法则，对于集合$G$中的每个复数$z=x+iy$，都有一个或几个复数$w=u+iv$与之对应，则称$w$是$z$的复变函数，记作$w=f(z)$

单值函数/多值函数
定义域：$G$
值域：$G^{*}$

复变函数$w=f(z)$确定了自变量为$x$和$y$的两个二元实变函数：$u=u(x,y),\ v=v(x,y)$

映射（把$z$平面上的点集$G$变到$w$平面上的点集$G^{*}$）、映像、原象

$w=f(z)$的反函数/逆映射：$z=\varphi(w)$

复变函数的极限与连续

极限的定义（$z\to z_0$的方式是任意的）
极限计算的定理

• 定理一：设$z_0=x_0+iy_0,\ f(z)=u(x,y)+iv(x,y),\ A=u_0+iv_0$，则$\lim_{z\to z_0}f(z)=A$的充要条件是：$\lim_{x\to x_0,y\to y_0}u(x,y)=u_0,\ \lim_{x\to x_0,y\to y_0}v(x,y)=v_0$
• 定理二：四则运算

连续的定义：$\lim_{z\to z_0}f(z)=f(z_0)$
连续的定理：

• 定理三：$f(z)=u(x,y)+iv(x,y)$在$z_0=x_0+iy_0$连续的充要条件是：$u(x,y)$和$v(x,y)$在$(x_0,y_0)$处连续
• 定理四：连续函数的和差积商、复合函数仍然连续

解析函数

导数的定义：极限$\lim_{\Delta z\to 0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$，其中$\Delta z\to 0$的方式是任意的
可导一定连续，连续不一定可导

解析的定义：若$f(z)$在$z_0$的某个邻域内处处可导，则称$f(z)$在$z_0$处解析
奇点：若$f(z)$在$z_0$不解析，则称$z_0$为$f(z)$的奇点
注意：

• 在某点处解析 强于 在某点处可导（反例：$f(z)=|z|^2$在$z_0=0$处可导但不解析）
• 在区域内解析 等价于 在区域内可导
  解析的定理：
• 解析函数的和差积商解析
• 复合函数的解析

可导的充要条件：
$f(z)=u(x,y)+iv(x,y)$在一点$z=x+iy$可导的充要条件：$u(x,y)$与$v(x,y)$在$(x,y)$可微，且满足柯西-黎曼方程（C-R方程）：$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\ \frac{\partial u}{\partial y}= - \frac{\partial v}{\partial x}$
导数公式：

$$f^{\prime}(z)=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}=\frac{1}{i}\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}$$

解析的充要条件：
$f(z)=u(x,y)+iv(x,y)$在定义域$D$内解析的充要条件：$u(x,y)$与$v(x,y)$在$D$内可微，且满足柯西-黎曼方程$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\ \frac{\partial u}{\partial y}= - \frac{\partial v}{\partial x}$

初等函数

指数函数

$$e^z=e^{x+iy}=e^x(\cos y+i\sin y)$$

• 复平面处处不为零
• 周期：$2k\pi i$
• 处处解析

对数函数

$$\text{Ln}z=\ln |z|+i\text{Arg}z=\ln|z|+i\text{arg}z+2k\pi i$$

• 多值函数
• 固定$k$，得到$\text{Ln}z$的第$k$个分支
• $k=0$时，称为主值
• 除去负实轴（包括原点）的复平面内，主值支和各分支处处连续、可导
• 应把$\text{Ln}z$视作集合记号，集合中有无穷个元素
  • $\text{Ln}z^n\ne n\text{Ln}z$
  • $\text{Ln}z+\text{Ln}z\ne 2\text{Ln}z$

幂函数

$$z^{\alpha}=e^{\alpha\text{Ln}z}=e^{\alpha(\ln|z|+i\text{Arg}z)}$$

• 多值函数
• 当$\alpha=\frac{m}{n}$为有理数时，为$n$值函数

三角函数

$$\cos z=\frac{e^{iz}+e^{-iz}}{2}$$ $$\sin z=\frac{e^{iz}-e^{-iz}}{2i}$$

• 周期：$2\pi$
• 在复平面内解析
• 无界!

双曲函数

$$\cosh z=\frac{e^z+e^{-z}}{2}$$ $$\sinh z=\frac{e^z-e^{-z}}{2}$$ $$\tanh z=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

• 周期：$2\pi i$
• $\sinh$奇函数，$\cosh$偶函数

反三角函数和反双曲函数

设$z=\cos w=\frac{e^{iw}+e^{-iw}}{2}$，得$e^{2iw}-2ze^{iw}+1=0$，解得：

$$w=\text{Arc}\cos z=-i\text{Ln}(z+\sqrt{z^2-1})$$

同理：

$$\text{Arc}\sin z=-i\text{Ln}(iz+\sqrt{1-z^2})$$ $$\text{Arc}\tan z=-\frac{i}{2}\text{Ln}\frac{1+iz}{1-iz}$$ $$\text{Arc}\sinh z=\text{Ln}(z+\sqrt{z^2+1})$$ $$\text{Arc}\cosh z=\text{Ln}(z+\sqrt{z^2-1})$$ $$\text{Arc}\tanh z=\frac{1}{2}\text{Ln}\frac{1+z}{1-z}$$

复变函数积分的概念

积分的定义

有向曲线、简单闭曲线的正向（逆时针）
积分的定义

$$\int_Cf(z)\mathrm{d}z=\lim_{n\to\infty}\sum_{k=1}^{n}f(\zeta_k)\cdot\Delta z_k$$

积分的计算

设$f(z)=u(x,y)+iv(x,y)$，则：

$$\int_Cf(z)\mathrm{d}z=\int_Cu(x,y)\mathrm{d}x-v(x,y)\mathrm{d}y+i\int_Cu(x,y)\mathrm{d}y+v(x,y)\mathrm{d}x$$

设$z(t)=x(t)+iy(t)$，则：

$$\int_Cf(z)\mathrm{d}z=\int_{\alpha}^{\beta}f[z(t)]z^{\prime}(t)\mathrm{d}t$$

重要结论：

$$\oint_{|z-z_0|=r}\frac{1}{(z-z_0)^{n+1}}\mathrm{d}z=\left\{\begin{matrix} 2\pi i, &n=0 \\\\ 0, &n\ne0 \end{matrix}\right.$$

积分中值定理不能直接推广到复变函数

柯西积分定理

柯西定理

若函数$f(z)$在单连通域$D$内处处解析，$C$为$D$内任意一条按段光滑曲线，则：

$$\int_Cf(z)\mathrm{d}z=0$$

多连通区域的柯西积分定理

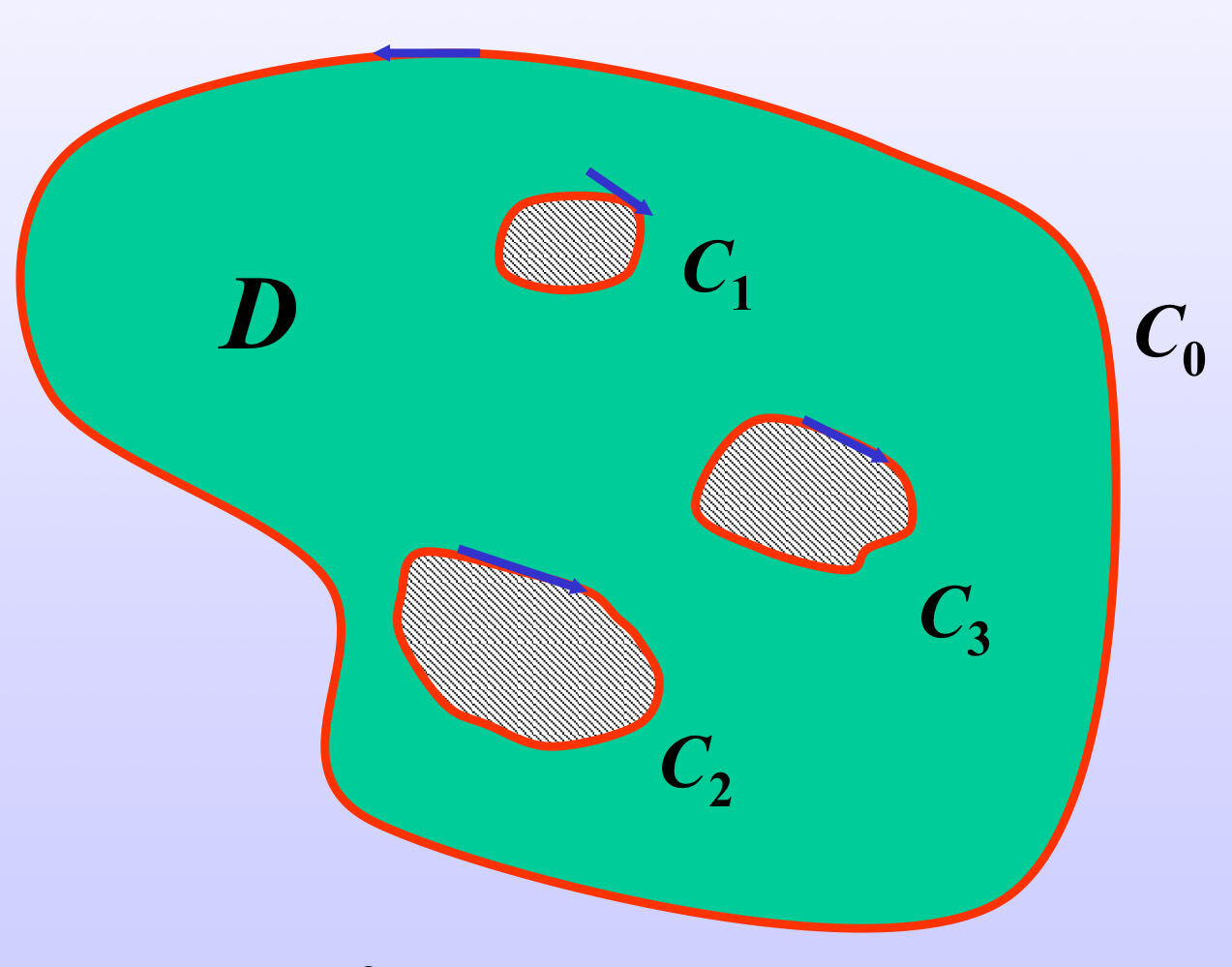
设$D$是由$n+1$条简单闭曲线$C_0,C_1,\dots,C_n$所围成的多连通区域，$C=C_0+C_1^-+\cdots+C_n^-$，函数$f(z)$在$D$内解析，在$\overline{D}=D+C$上连续，则：

$$\int_Cf(z)\mathrm{d}z=0$$

或：

$$\int_{C_0}f(z)\mathrm{d}z=\int_{C_1}f(z)\mathrm{d}z+\int_{C_2}f(z)\mathrm{d}z+\cdots+\int_{C_n}f(z)\mathrm{d}z$$

重要结论（$a$在简单闭曲线$\Gamma$内）：

$$\oint_{\Gamma}\frac{1}{(z-a)^{n+1}}\mathrm{d}z=\left\{\begin{matrix} 2\pi i, &n=0 \\\\ 0, &n\ne0 \end{matrix}\right.$$

解析函数的不定积分

定理：如果函数$f(z)$在单连通域$D$内处处解析，那么函数$F(z)=\int_{z_0}^zf(\zeta)\mathrm{d}\zeta$必为$D$内的一个解析函数，并且$F^{\prime}(z)=f(z)$

原函数与不定积分定义：设函数$f(z)$在区域$D$内连续，若$D$内的一个函数$\Phi(z)$满足$\Phi^{\prime}(z)=f(z)$，则称$\Phi(z)$为$f(z)$的一个原函数，$f(z)$的所有原函数的集合称为$f(z)$的不定积分

定理：若函数$f(z)$在区域$D$内处处解析，$\Phi(z)$为$f(z)$的一个原函数，那么：

$$\int_{z_0}^zf(z)\mathrm{d}z=\Phi(z)-\Phi(z_0)$$

柯西积分公式

定理：设函数$f(z)$在简单闭曲线$C$所围成的区域$D$内解析，在$\overline{D}=D+C$上连续，则对于$D$内任一点$z_0$，有：

$$f(z_0)=\frac{1}{2\pi i}\int_C\frac{f(z)}{z-z_0}\mathrm{d}z$$

平均值公式：若$C$是圆周$z=z_0+R\cdot e^{i\theta}$，则：

$$f(z_0)=\frac{1}{2\pi}\int_0^{2\pi}f(z_0+r\cdot e^{i\theta})\mathrm{d}\theta$$

一个解析函数在圆心处的值等于它在圆周上的平均值

该公式可以推广到多连通区域

高阶导数公式

高阶导数公式

定理：设函数$f(z)$在简单闭曲线$C$所围成的区域$D$内解析，在$\overline{D}=D+C$上连续，则$f(z)$在$D$内有各阶导数，且：

$$f^{(n)}(z_0)=\frac{n!}{2\pi i}\oint_C\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z$$

推论：设$f(z)$在复平面上的区域$D$内处处解析，则$f(z)$在$D$内具有各阶导数，且它们也在$D$内解析

柯西不等式

设$f(z)$在圆$|z-a|\le R$上解析，且$|f(z)|\le M(R)$，则有：

$$|f^{(n)}(a)|\le \frac{n!M(R)}{R^n}$$

刘维尔定理

有界整函数（整个复平面上解析）$f(z)$必为常数

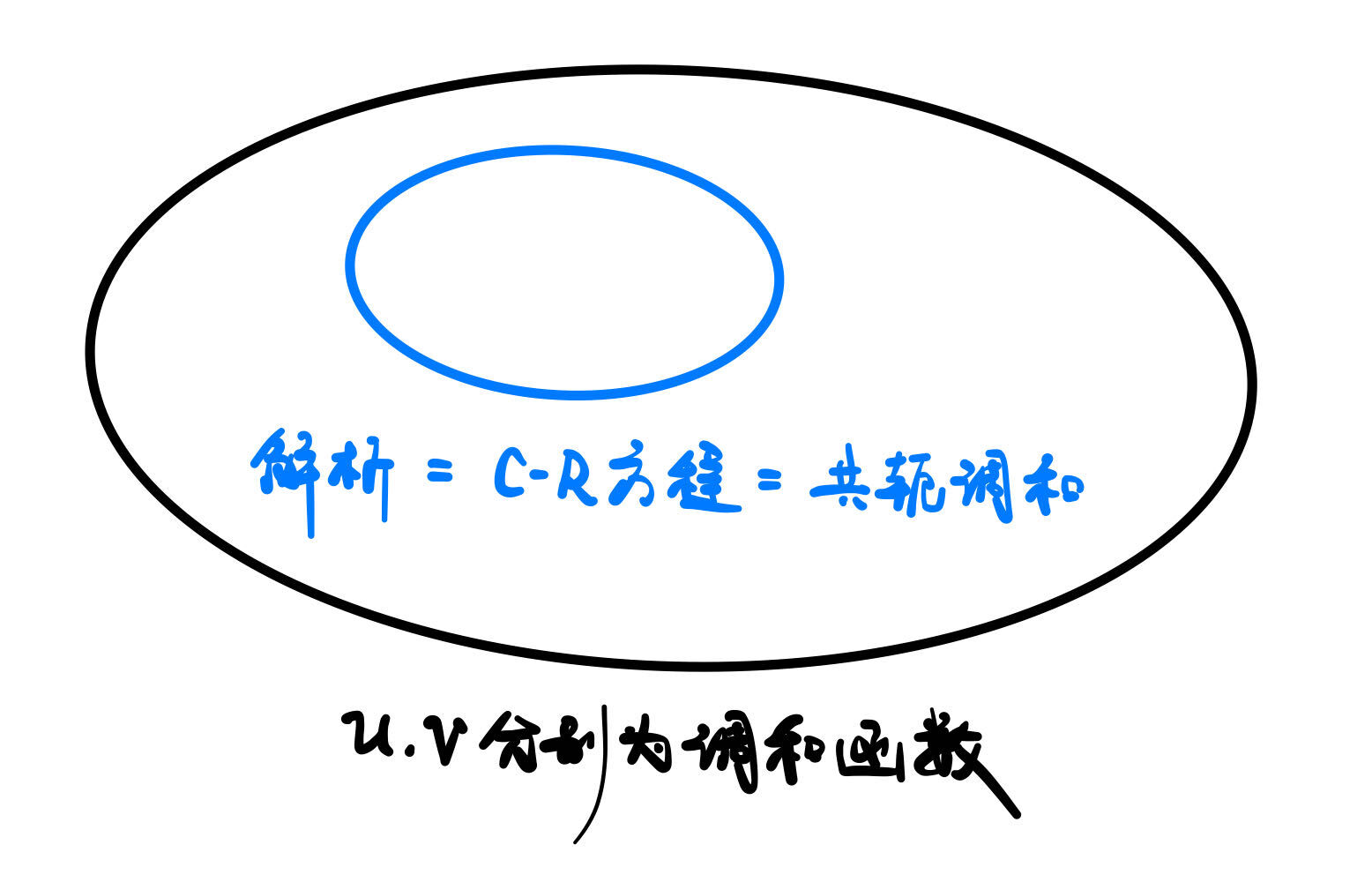
解析函数与调和函数

调和函数定义：如果二元实变函数$\varphi(x,y)$在区域$D$内具有二阶连续偏导数，并且满足拉普拉斯方程：

$$\frac{\partial^2\varphi}{\partial x^2}+\frac{\partial^2\varphi}{\partial y^2}=0$$

则称$\varphi(x,y)$为区域$D$内的调和函数，并记拉普拉斯算子：$\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}$

共轭调和函数定义：设$u(x,y), v(x,y)$都是区域$D$内的调和函数，若$u(x,y),v(x,y)$满足$C-R$方程，则称$v(x,y)$是$u(x,y)$的共轭调和函数（注意顺序）

定理：函数$f(z)=u+iv$在区域$D$内解析的充要条件：$v,u$是共轭调和函数

由调和函数求解析函数

1. 偏积分法：已知调和函数$u$，利用C-R方程求共轭调和函数$v$，得到解析函数$u+iv$
2. 不定积分法：由于$f^{\prime}(z)=u_x+iv_x=u_x-iu_y=v_y+iv_x$，则$f(z)=\int(u_x-iu_y)\mathrm{d}z+C$或$f(z)=\int(v_y+iv_x)\mathrm{d}z+C$

复级数

复数列的极限

定义
复数列收敛的充要条件：$\lim_{n\to\infty}a_n=a, \lim_{n\to\infty}b_n=b$

级数的概念

设$\{z_n\}=\{a_n+ib_n\}$为一复数列，表达式$\sum_{n=1}^{\infty}z_n=z_1+z_2+\cdots+z_n+\cdots$称为复数项无穷级数
$s_n=z_1+z_2+\cdots+z_n$称为级数的部分和
若部分和数列$\{s_n\}$收敛，则级数$\sum_{n=1}^{\infty}z_n$收敛，极限$\lim_{n\to\infty}s_n=s$称为级数的和

级数$\sum_{n=1}^{\infty}$收敛的充要条件：$\sum_{n=1}^{\infty}a_n$和$\sum_{n=1}^{\infty}b_n$都收敛
级数$\sum_{n=1}^{\infty}$收敛的必要条件：$\lim_{n\to\infty}z_n=0$

柯西收敛准则：
级数$\sum_{n=1}^{\infty}z_n$收敛的充要条件：对任给的$\varepsilon>0$，存在正整数$N$，使得$n>N$时，$p=1,2,\dots$时，有：

$$|\sum_{k=n}^{n+p}z_k|=|s_{n+p}-s_n|<\varepsilon$$

序列$\{z_n\}$收敛的充要条件：对任给的$\varepsilon>0$，存在正整数$N$，使得$m,n>N$时，有：

$$|z_m-z_n|<\varepsilon$$

绝对收敛、条件收敛
$\sum_{n=1}^{\infty}z_n$绝对收敛$\iff$$\sum_{n=1}^{\infty}a_n$与$\sum_{n=1}^{\infty}b_n$绝对收敛

复变函数项级数

定义：设$\{f_n(z)\}(n=1,2,\dots)$为一复变函数项序列，其中各项在区域$D$内有定义，表达式$\sum_{n=1}^{\infty}f_n(z)=f_1(z)+_2(z)+\cdots+f_n(z)+\cdots$称为复变函数项级数，记作$\sum_{n=1}^{\infty}f_n(z)$，$s_n(z)=f_1(z)+f_2(z)+\cdots+f_n(z)$称为部分和
若对于$D$内的某一点$z_0$，极限$\lim_{n\to\infty}s_n(z_0)=s(z_0)$存在，则称级数$\sum_{n=1}^{\infty}f_n(z)$在$z_0$收敛，且和为$s(z_0)$
若级数在$D$内处处收敛，则它的和为$z$的一个函数$s(z)=f_1(z)+f_2(z)+\cdots+f_n(z)+\cdots$，称为该级数在区域$D$上的和函数

幂级数

幂级数的概念

$$\sum_{n=0}^{\infty}c_n(z-a)^n=c_0+c_1(z-a)+c_2(z-a)^2+\cdots+c_n(z-a)^n+\cdots$$

称为以$a$为中心的幂级数

幂级数的敛散性

阿贝尔(Abel)定理：
若级数$\sum_{n=0}^{\infty}c_nz^n$在$z=z_0(\ne0)$收敛，则对满足$|z|<|z_0|$的$z$，级数必然绝对收敛；若级数在$z=z_0$发散，则对满足$|z|>|z_0|$的$z$，级数必然发散

收敛圆与收敛半径：
幂级数的收敛范围是一个圆域，级数在圆内绝对收敛，在圆外发散
收敛半径的三种情况：

• 全体正实数
• $z=0$
• 一个范围内收敛，范围外发散
  幂级数在收敛圆周上的敛散性不一定

收敛半径的求法：

• 比值法：若$\lim_{n\to\infty}|\frac{c_{n+1}}{c_n}|=\lambda\ne0$，则收敛半径$R=\frac{1}{\lambda}$
• 根植法：若$\lim_{n\to\infty}\sqrt[n]{|c_n|}=\lambda\ne0$，则收敛半径$R=\frac{1}{\lambda}$

幂级数的运算和性质

复变幂级数在收敛圆内的性质：
在收敛圆内，幂级数的和函数解析，可逐项求导，可逐项积分

泰勒级数

泰勒定理

设$f(z)$在圆域$K:|z-z_0|<R$内解析，则$f(z)$在$K$内可以展成唯一的正幂项幂级数

$$f(z)=\sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(z_0)(z-z_0)^n,\ \ n=0,1,2,\dots$$

定理：函数$f(z)$在$z_0$解析$\iff$$f(z)$在$z_0$的邻域内可以展开成幂级数
定理：幂级数的和函数在它的收敛圆轴上至少有一个奇点
推论：收敛半径$R$为$z_0$到最近一个奇点的距离

将函数展开成泰勒级数

1. 直接法
2. 间接法
   1. 换元法
   2. 逐项积分、求导法
   3. 微分方程法
   4. 柯西乘积
   5. 幂级数的四则运算

解析函数的唯一性定理

定理：
若$f(z)$在$|z-z_0|<R$内解析且不恒为0，$z_0$为其零点，则存在$z_0$的一个邻域，$f(z)$在此邻域中没有其他零点
引理：
设$f(z)$在区域$D$内解析，$\{z_n\}$是$D$内彼此不同的点列，且$\{z_n\}$在$D$内有聚点，若$f(z_n)=0\ (n=1,2,\dots)$，则在$D$内，$f(z)\equiv0$
唯一性定理：
设$f(z),g(z)$在区域$D$内解析，$\{z_n\}$是$D$内彼此不同的点列，且$\{z_n\}$在$D$内有聚点，若$f(z_n)=g(z_n)\ (n=1,2,\dots)$，则在$D$内，$f(z)\equiv g(z)$
推论：
设$f(z),g(z)$在区域$D$内解析，若它们在某一子区域或某一子弧段相等，则在$D$内相等

最大模原理

定理：
若$f(z)$在区域$D$内解析，且不为常数，则$|f(z)|$在$D$内取不到最大值
推论：

1. 若$f(z)$在区域$D$内解析，$D+C$上连续，则$|f(z)|$在$C$上取到最大值
2. 若$f(z)$在区域$D$内解析，且不为常数，则$Re[f(z)]$在$D$内取不到最大值
3. 若$f(z)$在区域$D$内解析，且不为常数，则$|f(z)|$在$D$内取不到最小值

洛朗级数

洛朗级数的概念

定理：
设$f(z)$在圆环域$R_1<|z-z_0|<R_2$内处处解析，，则$f(z)$在$D$可展开成唯一的正负幂项洛朗级数

$$f(z)=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n,\ \ c_n=\frac{1}{2\pi i}\oint_C\frac{f(\zeta)}{(\zeta-z_0)^{n+1}}\mathrm{d}\zeta\ \ (n=0,\pm1,\pm2,\dots)$$

$c_n$为洛朗系数，$C$为圆环域内绕$z_0$的任一条正向简单闭曲线

说明：

1. $z_0$可能是函数$f(z)$的奇点，也可能不是
2. 给定$f(z)$与$z_0$后，函数在不同圆环域中有不同的洛朗展开式

函数的洛朗展开式

1. 直接法
2. 间接法：代数运算、代换、求导、积分…

孤立奇点

概念与分类

孤立奇点的概念：
若$f(z)$在$z_0$不解析，但在$z_0$的某一去心邻域$0<|z-z_0|<\delta$内处处解析，则称$z_0$为$f(z)$的孤立奇点
孤立奇点的分类：

1. 可去奇点
   1. 定义：去心邻域的洛朗级数中不含$z-z_0$的负幂项
   2. 充要条件：$\lim_{z\to z_0}f(z)$存在且有限
2. $m$级极点
   1. 定义：去心邻域的洛朗级数中只有有限多个$z-z_0$的负幂项，且最小的负幂次为$-m$
   2. 充要条件：在去心邻域内$f(z)=\frac{\varphi(z)}{(z-z_0)^m}$，其中$\varphi(z)$在$z_0$解析且不为0
   3. 充要条件：$g(z)=\frac{1}{f(z)}$在$z_0$解析且是$m$级零点
   4. 特点：$\lim_{z\to z_0}f(z)=\infty$
3. 本性奇点
   1. 定义：去心邻域的洛朗级数中含无穷多个$z-z_0$的负幂项
   2. 特点：$\lim_{z\to z_0}f(z)$不存在且不为$\infty$

函数在无穷远点的性态

定义：若$f(z)$在无穷远点$z=\infty$的去心邻域$R<|z|<+\infty$内解析，则称$\infty$为$f(z)$的孤立奇点

令变换$t=\frac{1}{z}$，则$f(z)=f(\frac{1}{t})=\varphi(t)$，对$f(z)$无穷远点的研究转化为对$\varphi(t)$在$t=0$处的研究

留数

留数的引入

设$z_0$为$f(z)$的一个孤立奇点，$C$为$z_0$的某去心邻域$0<|z-z_0|<R$内包含$z_0$的任一简单闭曲线，则$f(z)$在邻域内有洛朗级数：

$$f(z)=\cdots+c_{-n}(z-z_0)^{-n}+\cdots+c_{-1}(z-z_0)^{-1}+c_0+c_1(z-z_0)+\cdots+c_n(z-z_0)^n+\cdots$$

故积分：

$$\oint_Cf(z)\mathrm{d}z=0(高阶导数公式)+2\pi i c_{-1}(c_{-1}\oint_C(z-z_0)^{-1}\mathrm{d}z)+0(柯西定理)$$

记：

$$c_{-1}=\frac{1}{2\pi i}\oint_Cf(z)\mathrm{d}z=\text{Res}[f(z),z_0]$$

为$f(z)$在$z_0$处的留数

利用留数求积分

留数定理：
函数$f(z)$在区域$D$内除有限个孤立奇点$z_1,z_2,\dots,z_n$外处处解析，$C$是$D$内包围诸奇点的一条正向简单闭曲线，则：

$$\oint_Cf(z)\mathrm{d}z=2\pi i\sum_{k=1}^n\text{Res}[f(z),z_k]$$

留数的计算方法：

1. 若$z_0$为可去奇点：$\text{Res}[f(z),z_0]=0$；
2. 若$z_0$为本性奇点：需要展开成洛朗级数求$c_{-1}$；
3. 若$z_0$为$n$级极点：（先除掉所有负幂项，再通过求导剩下$c_{-1}$） $$\text{Res}[f(z),z_0]=\frac{1}{(n-1)!}\lim_{z\to z_0}\frac{\mathrm{d}^{n-1}}{\mathrm{d}z^{n-1}}[(z-z_0)^nf(z)]$$

在无穷远点的留数

$$\text{Res}[f(z),\infty]=\frac{1}{2\pi i}\oint_{C^-}f(z)\mathrm{d}z=-\frac{1}{2\pi i}\oint_Cf(z)\mathrm{d}z=-c_{-1}$$

其中，$C$是在$R<|z|<+\infty$圆环域中的正向简单闭曲线

定理：
若$f(z)$在扩充复平面内只有有限个孤立奇点，则$f(z)$在所有奇点（包括$\infty$点）的留数之和等于0

Fourier变换

积分变换：通过积分运算，把一个函数变成另一个函数的变换，一般是参变量$\alpha$的积分

$$F(\alpha)=\int_a^bf(t)K(t,\alpha)\mathrm{d}t$$

其中，$K(t,\alpha)$是一个确定的二元函数，称为积分变换的核
选取不同的积分域和变换核，就可得到不同的积分变换

广义积分收敛：设函数$f(t)$在实轴的任何有限区间上都可积，若极限$\lim_{R\to+\infty}\int_{-R}^Rf(t)\mathrm{d}t$存在，则称在主值意义下$f(t)$在区间$(-\infty,+\infty)$上的广义积分收敛，记为：$P.V.\int_{-\infty}^{+\infty}f(t)\mathrm{d}t=\lim_{R\to+\infty}\int_{-R}^Rf(t)\mathrm{d}t$

Fourier级数

一个以$T$为周期的函数$f_T(t)$，若在$[-\frac{T}{2},\frac{T}{2}]$上满足Dirichlet条件：

• 连续或只有有限个间断点
• 有限个极值点
  那么，在$[-\frac{T}{2},\frac{T}{2}]$上就可以展成Fourier级数：
  在$f_T(t)$的连续点处，级数的三角形式： $$f_T(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos n\omega t+b_n\sin n\omega t)$$ 其中， $$\omega=\frac{2\pi}{T},\ a_0=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)\mathrm{d}t$$ $$a_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)\cos n\omega t\mathrm{d}t\ (n=1,2,\dots)$$ $$b_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)\sin n\omega t\mathrm{d}t\ (n=1,2,\dots)$$

令$A_0=a_0,\ A_n=\sqrt{a_n^2+b_n^2}$，则：

$$f_T(t)=\frac{A_0}{2}+\sum_{n=1}^{\infty}A_n\sin(n\omega t+\theta_n)$$

其中，$A_n$称为振幅
计算级数的复指数形式：

$$\begin{align*} f_T(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}[a_n\frac{e^{in\omega t}+e^{-in\omega t}}{2}+b_n\frac{e^{in\omega t}-e^{-in\omega t}}{2i}]\\\\ &=\frac{a_0}{2}+\sum_{n=1}^{\infty}[\frac{a_n-ib_n}{2}e^{in\omega t}+\frac{a_n+ib_n}{2}e^{-in\omega t}] \end{align*}$$

令：

$$\begin{align*} c_0&=\frac{a_0}{2}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)\mathrm{d}t\\\\ c_n&=\frac{a_n-ib_n}{2}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)e^{-in\omega t}\mathrm{d}t\ \ (n=1,2,\dots)\\\\ c_{-n}&=\frac{a_n+ib_n}{2}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)e^{in\omega t}\mathrm{d}t\ \ (n=1,2,\dots) \end{align*}$$

合成一个式子：

$$c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)e^{-in\omega t}\mathrm{d}t\ \ (n=0,\pm1,\pm2,\dots)$$ $$|c_n|=\frac{1}{2}\sqrt{a_n^2+b_n^2}$$

则级数的复指数形式为：

$$f_T(t)=c_0+\sum_{n=1}^{\infty}[c_ne^{in\omega t}+c_{-n}e^{-in\omega t}]=\sum_{n=-\infty}^{+\infty}c_ne^{in\omega t}$$

故$A_n=2|c_n|$称为周期函数$f_T(t)$的振幅频谱/离散频谱

Fourier变换

非周期函数$f(t)$可以看作某个周期函数$f_T(t)$当$T\to+\infty$时转化而来，故：

$$\begin{align*} f(t)=\lim_{T\to+\infty}f_T(t)&=\lim_{T\to+\infty}\sum_{n=-\infty}^{+\infty}c_ne^{in\omega t}=\lim_{T\to+\infty}\frac{1}{T}\sum_{n=-\infty}^{+\infty}[\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(\tau)e^{-i\omega_n\tau}\mathrm{d}\tau]e^{i\omega_nt}\\\\ &=\lim_{\Delta\omega_n\to0}\frac{1}{2\pi}\sum_{n=-\infty}^{+\infty}[\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(\tau)e^{-i\omega_n\tau}\mathrm{d}\tau]e^{i\omega_nt}\Delta\omega_n \end{align*}$$

注意，此时$\omega=\frac{2\pi}{T}$很小，$\omega_n=\omega n$均匀分布到整个数轴上

Fourier积分定理：
若$f(t)$在$(-\infty,+\infty)$上满足下列条件：

• 在任一有限区间上满足Dirichlet条件
• 在$(-\infty,+\infty)$上绝对可积
  那么在连续点处有： $$f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}f(\tau)e^{-i\omega\tau}\mathrm{d}\tau]e^{i\omega t}\mathrm{d}\omega$$ 在间断点处有： $$f(t)=\frac{f(t+0)+f(t-0)}{2}$$ 故： $$F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}\mathrm{d}t$$ $$f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}\mathrm{d}\omega$$ 称$F(\omega)$为$f(t)$的频谱函数/连续频谱

一些常用函数的Fourier变换

$\delta$函数

狄拉克的定义，满足下列两个条件：

1. $\delta(t)=0\ \ (t\ne0)$
2. $\int_{-\infty}^{+\infty}\delta(t)\mathrm{d}t=1$

数学定义：

1. 定义1：对任何一个无穷次可微函数$f(t)$，若满足 $$\int_{-\infty}^{+\infty}\delta(t)f(t)\mathrm{d}t=\lim_{\varepsilon\to0}\int_{-\infty}^{+\infty}\delta_{\varepsilon}(t)f(t)\mathrm{d}t$$ 其中， $$\delta_{\varepsilon}(t)=\left\{\begin{matrix} 0,&t<0 \\\\ \frac{1}{\varepsilon},&0\le t\le\varepsilon \\\\ 0,&t>\varepsilon \end{matrix}\right.$$ 则称$\delta_{\varepsilon}(t)$的弱极限为$\delta$函数，记为$\delta(t)$
2. 定义2：若对于$(-\infty,+\infty)$的任意一个区间上连续的函数$f(t)$都有： $$\int_{-\infty}^{+\infty}\delta(t-t_0)f(t)\mathrm{d}t=f(t_0)$$ 则称$\delta(t)$为$\delta$函数
3. 定义2可由定义1推出

其他性质：

1. 偶函数
2. 积分为单位阶跃函数$u(t)=\int_{-\infty}^t\delta(\tau)\mathrm{d}\tau$
   3.若$f(t)$为无穷次可微的函数，则有$\int_{-\infty}^{+\infty}\delta^{(n)}(t)f(t)\mathrm{d}t=(-1)^nf^{(n)}(0)$

广义Fourier变换

$$\mathfrak{F}[\delta(t)]=1$$ $$\mathfrak{F}^{-1}[2\pi\delta(\omega)]=1$$ $$\mathfrak{F}[u(t)]=\frac{1}{i\omega}+\pi\delta(\omega)$$

Fourier变换的性质

重要性质

1. 线性性质
2. 时移性质：$\mathfrak{F}[f(t\pm t_0)]=e^{\pm i\omega t_0}F(\omega)$
3. 频移性质：$\mathfrak{F}[f(t)e^{\pm i\omega_0t}]=F(\omega\mp\omega_0)$
4. 时域微分性质：若$f^{(k)}(t)$在$(-\infty,+\infty)$上连续或只有有限个可去间断点，且$\lim_{|t|\to+\infty}f^{(k)}(t)=0, \ k=0,1,\dots,n-1$，则$\mathfrak{F}[f^{(n)}(t)]=(i\omega)^nF(\omega)$
5. 频域微分性质：$\frac{\mathrm{d}^n}{\mathrm{d}\omega^n}F(\omega)=(-i)^n\mathfrak{F}[t^nf(t)]$
6. 时域积分性质：若$t\to+\infty$时，$g(t)=\int_{-\infty}^tf(t)\mathrm{d}t\to0$，则$\mathfrak{F}[\int_{-\infty}^tf(t)\mathrm{d}t]=\frac{1}{i\omega}F(\omega)$

   一般情况下，$\mathfrak{F}[\int_{-\infty}^tf(t)\mathrm{d}t]=\frac{F(\omega)}{i\omega}+\pi F(0)\delta(\omega)$
   

7. 对称性质：若$\mathfrak{F}[f(t)]=F(\omega)$，则$\mathfrak{F}[F(t)]=2\pi f(-\omega)$
8. 压扩性质：$\mathfrak{F}[f(at)]=\frac{1}{|a|}F(\frac{\omega}{a})$
9. 压扩+时移性质：$\mathfrak{F}[f(at+b)]=\frac{1}{|a|}e^{i\frac{b}{a}\omega}F(\frac{\omega}{a})$
10. 乘积定理：$\int_{-\infty}^{+\infty}f_1(t)f_2(t)\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\overline{F_1(\omega)}F_2(\omega)\mathrm{d}\omega=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F_1(\omega)\overline{F_2(\omega)}\mathrm{d}\omega$
11. 帕塞瓦尔定理：$\int_{-\infty}^{+\infty}[f(t)]^2\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}|F(\omega)|^2\mathrm{d}\omega$

卷积

卷积概念：$f_1(t)f_2(t)=\int_{-\infty}^{+\infty}f_1(\tau)f_2(t-\tau)\mathrm{d}\tau$
交换律、结合律、分配律
$|f_1(t)f_2(t)|\le|f_1(t)|*|f_2(t)|$

卷积定理：$\mathfrak{F}[f_1(t)f_2(t)]=F_1(\omega)F_2(\omega)\ \ \ \ \mathfrak{F}[f_1(t)\cdot f_2(t)]=\frac{1}{2\pi}F_1(\omega)F_2(\omega)$

Fourier变换的应用

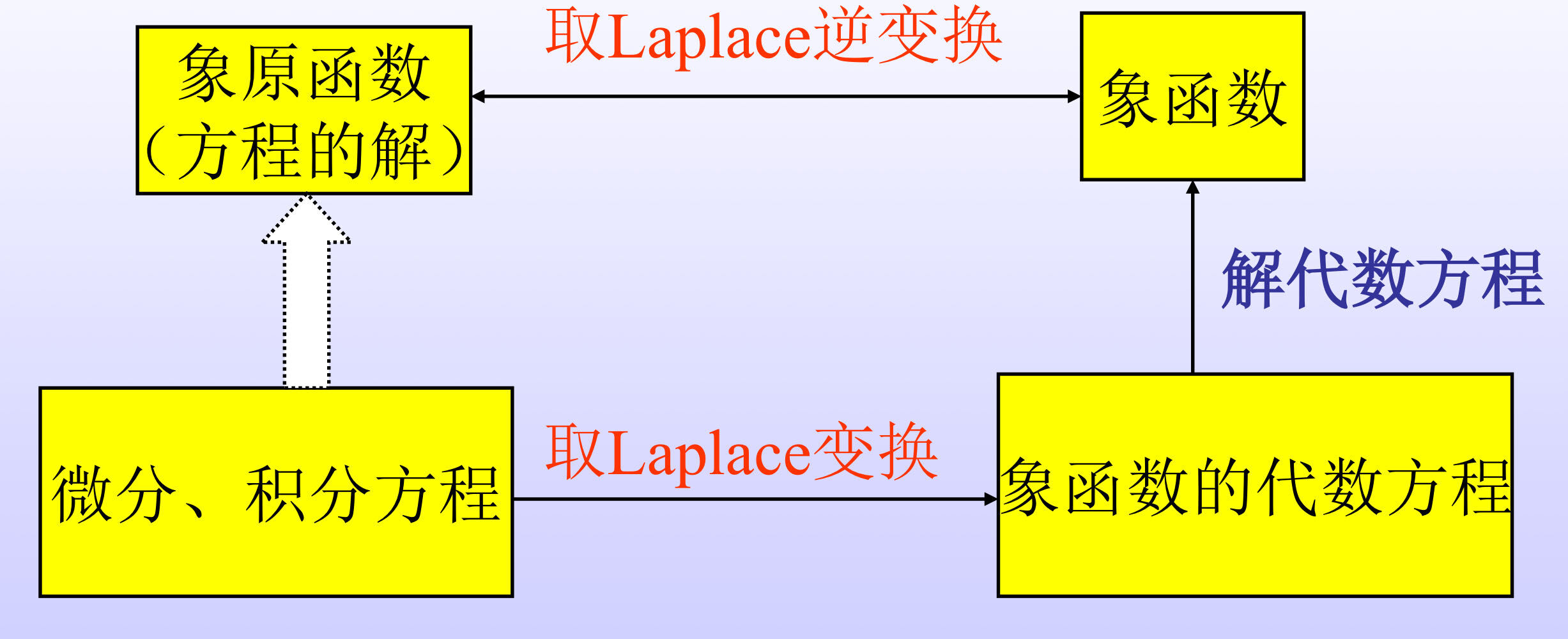
微分、积分方程的Fourier变换解法

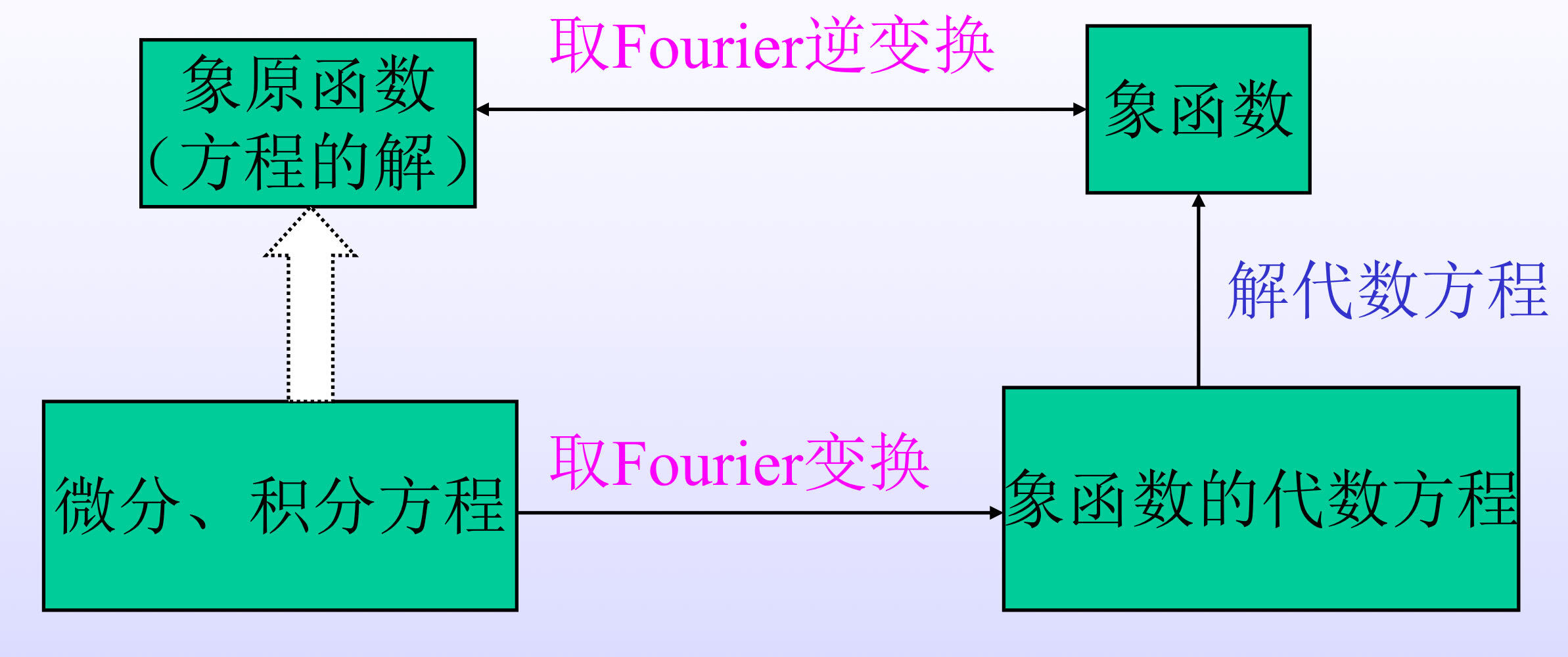
傅里叶变换在电路方面的应用

$$u=Ri,\ \ \ \ i=C\frac{\mathrm{d}u}{\mathrm{d}t},\ \ \ \ u=L\frac{\mathrm{d}i}{\mathrm{d}t}$$ $$U=RI,\ \ \ \ I=i\omega CU,\ \ \ \ U=i\omega LI$$

复阻抗：$Z=\frac{U}{I}=R\ or\ \frac{1}{i\omega C}\ or\ i\omega L$

傅里叶变换在通讯方面的应用

离散傅里叶变换在信号处理及图像处理中的应用

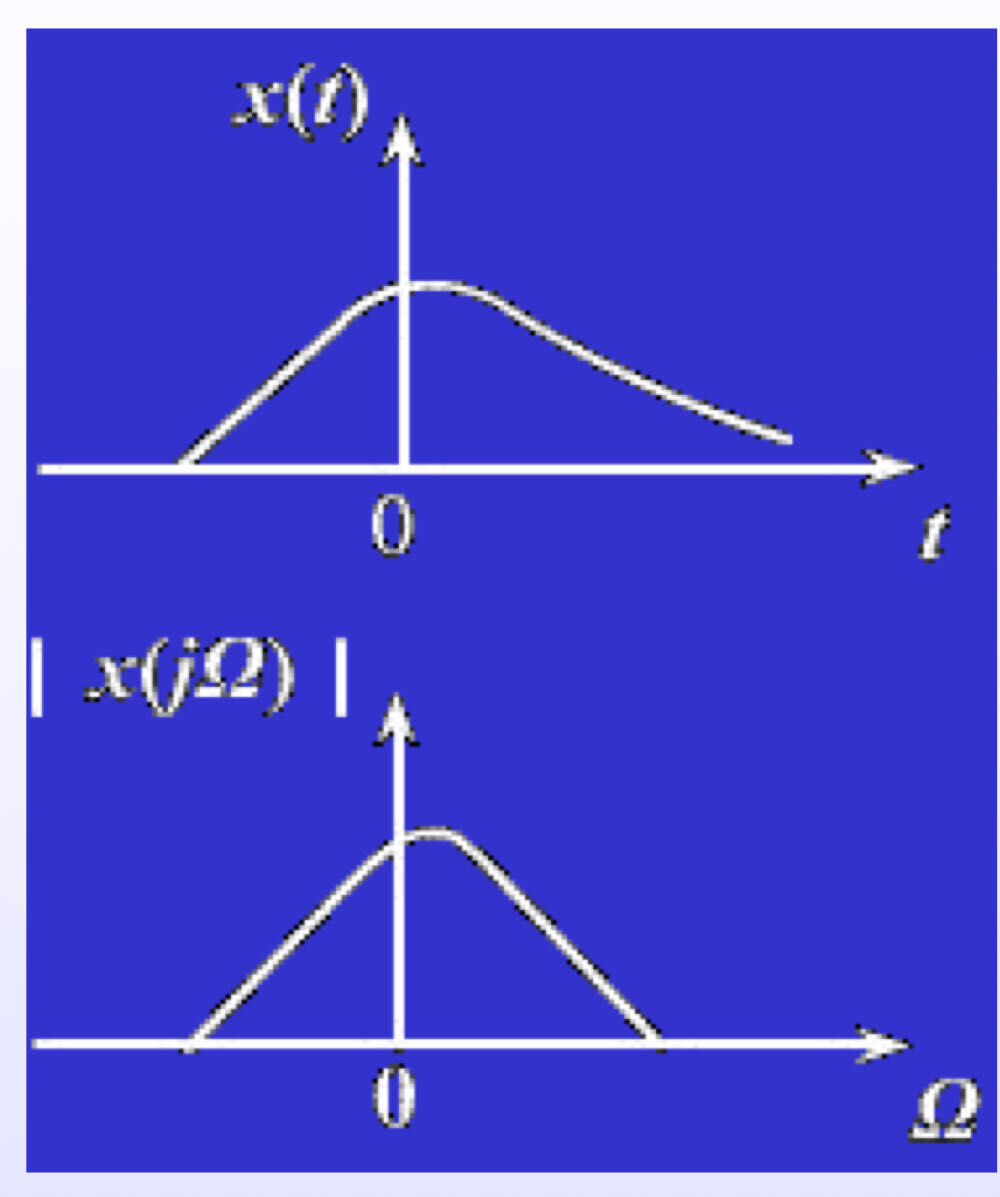
• 连续时间、连续频率 —— 傅里叶变换（FT）
  • 时域连续 $\to$ 频域非周期
  • 时域非周期 $\to$ 频域连续
  • $$\begin{align*} X(j\Omega)&=\int_{-\infty}^{+\infty}x(t)e^{-j\Omega t}\mathrm{d}t\\\\ x(t)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\Omega)e^{j\Omega t}\mathrm{d}\Omega \end{align*}$$
  • 
• 连续时间、离散频率 —— 傅里叶级数（DFS）
  • 时域连续 $\to$ 频域非周期
  • 时域周期 $\to$ 频域离散
  • $$\begin{align*} f_T(t)&=\sum_{n=-\infty}^{+\infty}c_ne^{in\omega t}\\\\ c_n&=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_T(t)e^{-in\omega t}\mathrm{d}t\ \ (n=0,\pm1,\pm2,\dots) \end{align*}$$
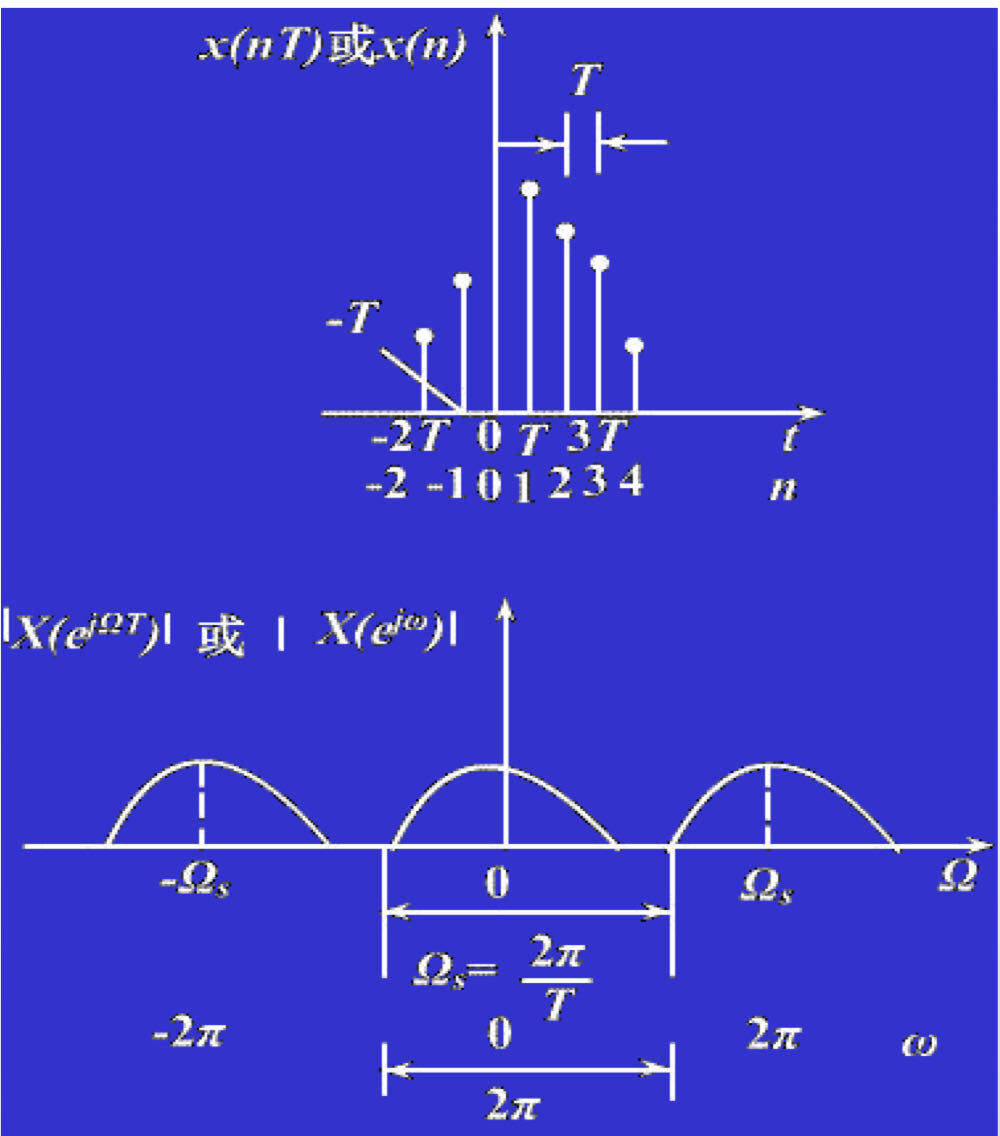
• 离散时间、连续频率 —— 序列的傅里叶变换（DTFT）
  • 时域离散 $\to$ 频域周期延拓
  • 时域非周期 $\to$ 频域连续
  • $$\begin{align*} X(e^{j\omega})&=\sum_{n=-\infty}^{+\infty}x(n)e^{-j\omega n}\\\\ x(n)&=\frac{1}{2\pi}\int_{-\pi}^{+\pi}X(e^{j\omega})e^{j\omega n}\mathrm{d}\omega \end{align*}$$
  • 
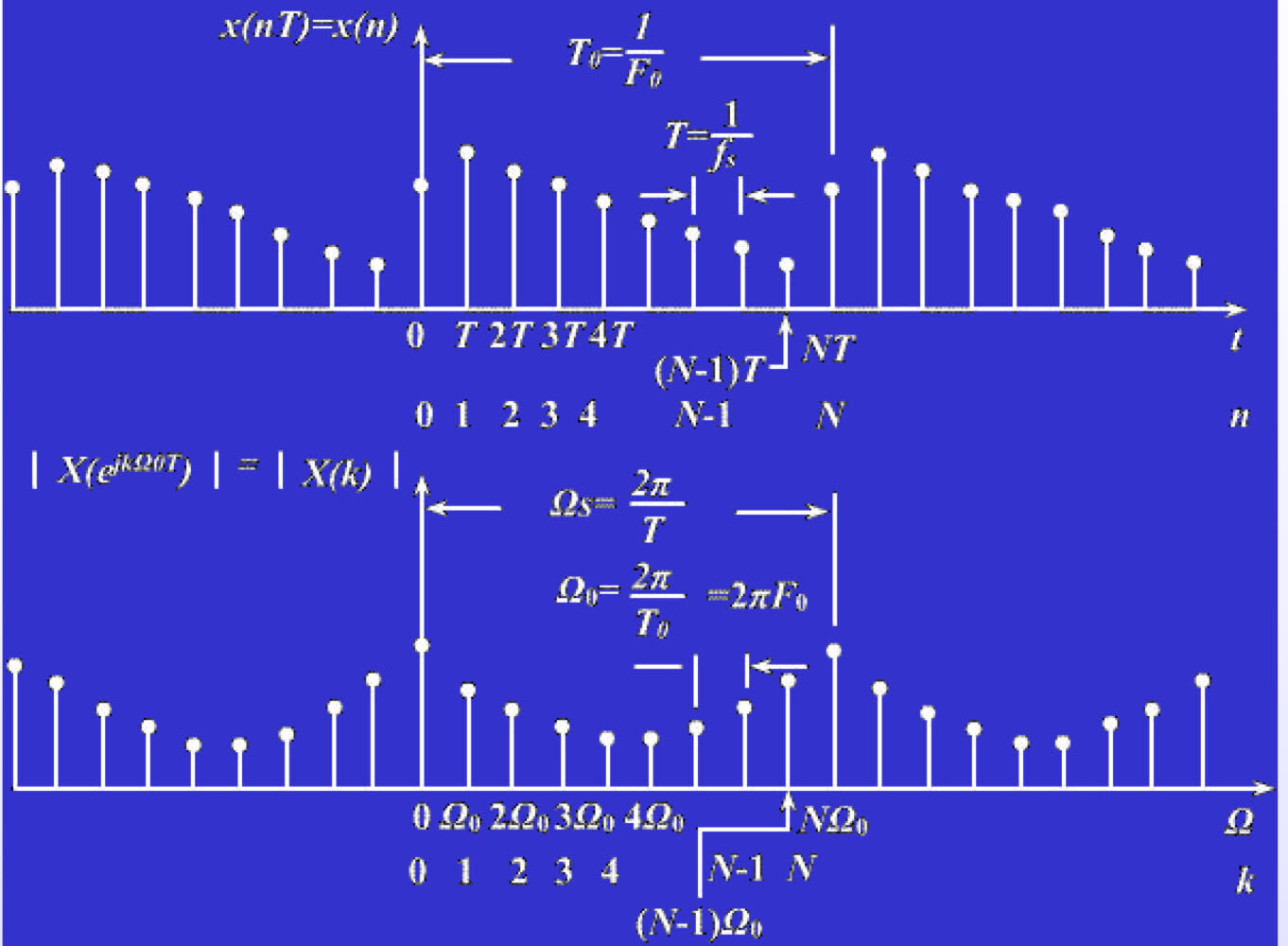
• 离散时间、离散频率 —— 离散傅里叶变换（DFT）
  • 时域离散 $\to$ 频域周期延拓
  • 时域周期延拓 $\to$ 频域离散
  • $$\begin{align*} X(k)&=\sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}nk},\ \ &0\le k\le N-1\\\\ x(n)&=\frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{j\frac{2\pi}{N}nk},\ \ &0\le n\le N-1 \end{align*}$$
  • 

数字信号传输的优点：抗干扰能力强、信号还原质量高、易于加密和解密
但是，需要$\Delta t$取得很小，$N$非常大；所以，需要对数据序列进行简化和压缩
DFT的优点：抗干扰能力进一步提高、使需传输的序列大为缩短、易于作高效的压缩处理

快速傅里叶变换（FFT）

时域抽取法（DIT-FFT）

频域抽取法（DIF-FFT）

Laplace变换的概念

$f(t)$的Laplace变换 $\iff$ $f(t)u(t)e^{-\beta t}$的Fourier变换

设函数$f(t)$当$t\ge 0$时有意义，且积分$\int_0^{+\infty}f(t)e^{-st}\mathrm{d}t$（$s$是一个复参数）在$s$的某一个域内收敛，则该积分记作$F(s)$称为Laplace变换式：

$$F(s)=\mathfrak{L}[f(t)]=\int_0^{+\infty}f(t)e^{-st}\mathrm{d}t$$

注意：严格来说，要注明$s$的收敛域

Laplace变换的存在定理（充分条件）：
若$f(t)$满足下列条件：

1. 在$t\ge0$的任一有效区间上分段连续；
2. 当$t\to+\infty$时，$f(t)$的增长速度不超过某一指数函数，亦即存在常数$M\ge0$及$c\ge0$，使得$|f(t)|\le Me^{ct},\ 0\le t<+\infty$成立
   则$f(t)$的Laplace变换$F(s)=\int_0^{+\infty}f(t)e^{-st}\mathrm{d}t$在$Re(s)>c$上一定存在且为解析函数，右端积分在$Re(s)\ge c_1>c$上绝对且一致收敛

以$T$为周期的函数$f(t)$，当$f(t)$在一个周期上分段连续时：

$$\mathfrak{L}[f(t)]=\frac{1}{1-e^{-sT}}\int_0^Tf(t)e^{-st}\mathrm{d}t\ \ (Re(s)>0)$$

Laplace变换的性质

重要性质

1. 线性性质
2. 时域微分：$\mathfrak{L}[f^{\prime}(t)]=sF(s)-f(0)$

     $\mathfrak{L}[f^{(n)}(t)]=s^nF(s)-s^{n-1}f(0)-s^{n-2}f^{\prime}(0)-\cdots-f^{(n-1)}(0)$
   

3. 频域微分：$\mathfrak{L}[-tf(t)]=F^{\prime}(s)$
   $\mathfrak{L}[(-t)^nf(t)]=F^{(n)}(s)$
4. 时域积分：$\mathfrak{L}[\int_0^tf(t)\mathrm{d}t]=\frac{1}{s}F(s)$
5. 频域积分：$\mathfrak{L}[\frac{f(t)}{t}]=\int_s^{+\infty} F(s)\mathrm{d}s$
6. 压扩性质：$\mathfrak{L}[f(at)]=\frac{1}{a}F(\frac{s}{a})$
7. 时移性质：$\mathfrak{L}[f(t\pm\tau)]=e^{\pm s\tau}F(s)$
8. 频移性质：$\mathfrak{L}[e^{\pm\alpha t}f(t)]=F(s\mp\alpha)$

卷积定理

$\mathfrak{L}[f_1(t)*f_2(t)]=F_1(s)\cdot F_2(s)$

Laplace逆变换

$$f(t)=\frac{1}{2\pi i}\int_{\beta-i\infty}^{\beta+i\infty}F(s)e^{st}\mathrm{d}s,\ \ t>0$$

若$s_1,s_2,\cdots,s_n$是函数$F(s)$的所有奇点（适当选取$\beta$使得这些奇点都在$Re(s)<\beta$的范围内），且当$s\to\infty$时$F(s)\to 0$，则有：

$$f(t)=\sum_{k=1}^{n}\underset{s=s_k}{\text{Res}}[F(s)e^{st}],\ \ t>0$$

推论：
设$F(s)=\frac{A(s)}{B(s)}$，其中$A(s),B(s)$是既约多项式，$B(s)$次数是$n$且大于$A(s)$次数，设极点为$s_1,s_2,\dots,s_k$，阶数分别为$p_1,p_2,\dots,p_k(\sum_{j=1}^kp_j=n)$，那么在$f(t)$的连续点处，有：

$$f(t)=\sum_{j=1}^k\frac{1}{(p_j-1)!}\lim_{s\to s_j}\frac{\mathrm{d}^{p_j-1}}{\mathrm{d}s^{p_j-1}}[(s-s_j)^{p_j}\frac{A(s)}{B(s)}e^{st}]$$

Laplace 变换的应用

微分、积分方程的Laplace变换解法