Understanding Diffusion Models - A Unified Perspective

Introduction

生成式模型：根据某分布的样本值 $x$建模分布$p(x)$，然后从该分布得到新样本值

当前生成式模型的方向：

• Generative Adversarial Networks（GANs）

• likelihood-based modeling

  • autoregressive models, normalizing flows, Variational Autoencoders（VAEs）
• energy-based modeling
• score-based modeling

diffusion models（扩散模型）既有likelyhood-based解释，也有score-based解释

Background: ELBO, VAE, and Hierarchical VAE

思想：将观察到的数据视为潜在随机变量$z$的“投影” （柏拉图《洞穴寓言》 ）

Evidence Lower Bound（ELBO）

证据下界，是变分推断（Variational Inference）中的核心概念

将$x$与$z$建模为联合分布$p(x,z)$

$p(x)=\int p(x,z)dz$ 或 $p(x)=\frac{p(x,z)}{p(z|x)}$

目标：最大化$p(x)$

但是两种方法都难以计算，提出ELBO（观测数据的对数似然的下界，evidence指$p(x)$），最大化ELBO：

$ELBO=\mathbb{E}_{q_\phi(z|x)}[\log\frac{p(x,z)}{q_\phi(z|x)}]\le\log p(x)$

$q_\phi(z|x)$是一个可调参$\phi$的变分分布，用来近似$p(z|x)$；$\mathbb{E}$代表求期望。上述等式可用Jensen不等式证明，但不直观。

另一种方法可证明：

$\log p(x)=\mathbb{E}_{q_\phi(z|x)}[\log\frac{p(x,z)}{q_\phi(z|x)}] + D_{KL}(q_\phi(z|x)||p(z|x))$

evidence是ELBO加上估计后验与真实后验之间的KL散度（非负）

在Autoencoder中，由于$\log p(x)$关于$\phi$是常数，最大化ELBO等价于最小化KL散度，等价于使 $q_\phi(z|x)$逼近 $p(z|x)$

KL散度（Kullback-Leibler divergence），又称作相对熵（relative entropy）或信息散度（information divergence）。KL散度的理论意义在于度量两个概率分布之间的差异程度，当KL散度越大的时候，说明两者的差异程度越大；而当KL散度小的时候，则说明两者的差异程度小。如果两者相同的话，则该KL散度应该为0。

设两个概率分布分别为P和Q，在设定为连续随机变量的前提下，KL散度可以表示为：

$KL(P||Q)=\int p(x)\log\frac{p(x)}{q(x)}dx$

Variational Autoencoders（VAEs）

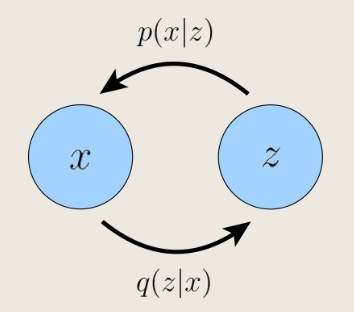
• 编码器：$q(z|x)$，观测值 -> 潜在变量
• 解码器：$p(x|z)$，潜在变量 -> 观测值

继续研究ELBO项：

$ELBO=\mathbb{E}_{q_\phi(z|x)}[\log\frac{p(x,z)}{q_\phi(z|x)}]=\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]-D_{KL}(q_\phi(z|x)||p(z))$

• 第一项：reconstruction term，确保学习到的分布的确能重构出观测数据，用Monte Carlo估计，最大化
• 第二项：prior matching term，确保学习到的分布不是Dirac函数（？），可解析计算，最小化，希望编码器得到尽量真实的潜在分布

通常选取的形式：

• $q_\phi(z|x)=\mathcal{N}(z;\mu_\phi(x),\sigma_\phi^2(x)\mathbf{I})$
• $p(z)=\mathcal{N}(z;\mathbf{0},\mathbf{I})$

因此，重写目标优化表达式：
$\underset{\phi,\ \theta}{argmax}\ ELBO \approx \underset{\phi,\ \theta}{argmax}\sum_{l=1}^{L}\log p_\theta(x|z^{(l)}) - D_{KL}(q_\phi(z|x)||p(z))$

对每个$x$，$z^{(l)}$从$q_\phi(z|x)$中采样得到

缺点：每个$z^{(l)}$从随机采样过程得到，一般不可微分

办法：重新参数化如下，优化$\mu_\phi$和$\sigma_\phi$

$z=\mu_\phi(x)+\sigma_\phi(x)\odot\epsilon\quad with\ \epsilon\sim\mathcal{N}(\epsilon;\mathbf{0},\mathbf{I})$

Hierarchical Variational Autoencoders（HVAEs）

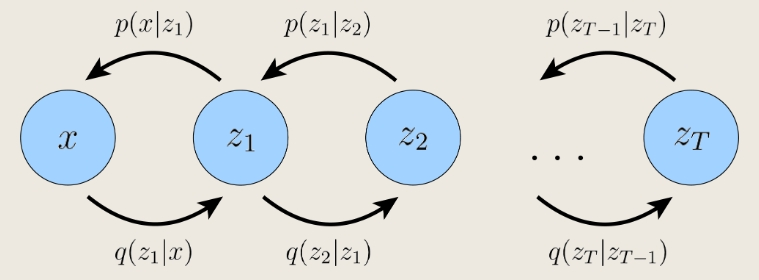
Markovian HVAE：每一层仅依赖于上一层，又称Recursive VAE

联合分布：$p(x,z_{1:T})=p_\theta(x|z_1)\prod_{t=2}^{T}p_\theta(z_{t-1}|z_t)p(z_T)$

后验概率：$q_\phi(z_{1:T}|x)=q_\phi(z_1|x)\prod_{t=2}^{T}q_\phi(z_t|z_{t-1})$

因此，ELBO：

$$\begin{align*} \log p(x) &\ge \mathbb{E}_{q_\phi(z_{1:T}|x)}[\log\frac{p(x,z_{1:T})}{q_\phi(z_{1:T}|x)}] \\ &= \mathbb{E}_{q_\phi(z_{1:T}|x)}[\log \frac{p_\theta(x|z_1)\prod_{t=2}^{T}p_\theta(z_{t-1}|z_t)p(z_T)}{q_\phi(z_{1:T}|x)=q_\phi(z_1|x)\prod_{t=2}^{T}q_\phi(z_t|z_{t-1})}] \end{align*}$$

Variational Diffusion Models（VDMs）

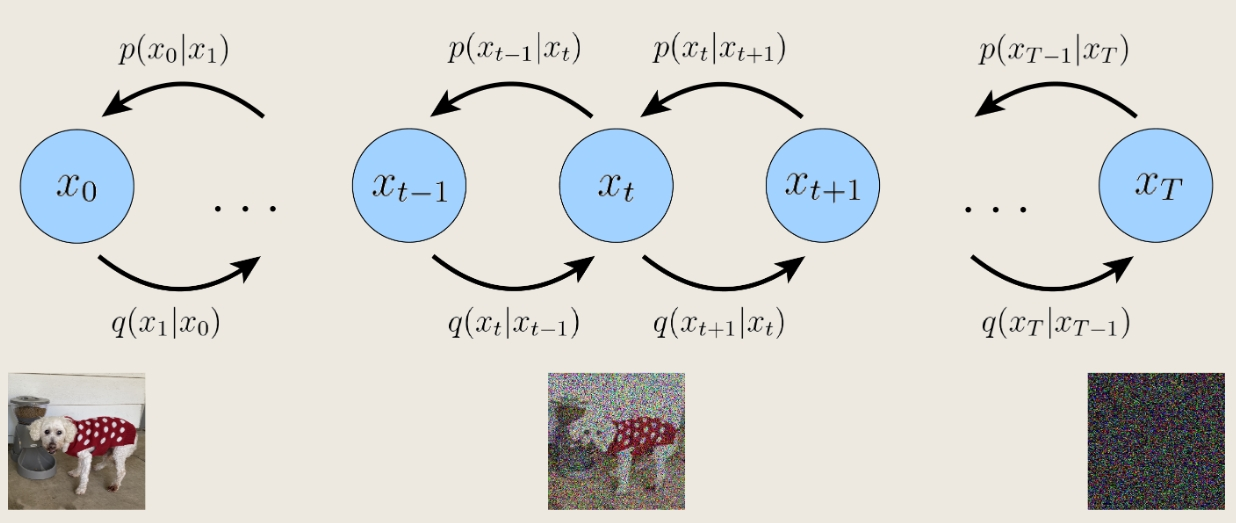
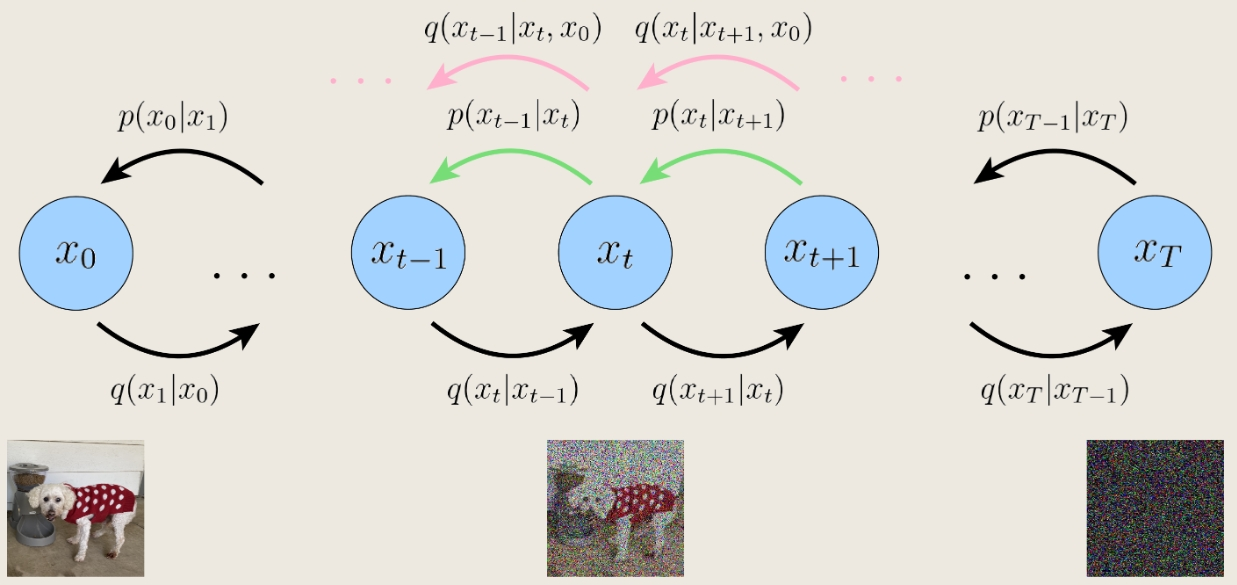
$x_0$是原图，$x_T$是标准高斯噪声，每幅图是上一副图的高斯分布（参数可学习）

联合分布：$p(x_{0:T})=p(x_T)\prod_{t=1}^{T}p_\theta(x_{t-1}|x_t)\quad where \ p(x_T)=\mathcal{N}(x_T;\mathbf{0},\mathbf{I})$

后验概率：$q(x_{1:T}|x_0)=\prod_{t=1}^{T}q(x_t|x_{t-1})$

编码过程：$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf{I})$，$\alpha_t$按制定规则演化或可学习

思想：编码过程是一步步添加高斯噪声破坏原图（为纯高斯噪声）的过程

编码过程$q(x_t|x_{t-1})$是确定的，故只需要学习解码过程 $p_\theta(x_{t-1}|x_t)$，最终实现从高斯噪声中采样、解码、生成新图像

故ELBO可表示为：

$$\begin{align*} \log p(x_0) &\ge \mathbb{E}_{q(x_{1:T}|x_0)}[\log \frac{p(x_{0:T})}{q(x_{1:T}|x_0)}] \\ &= \mathbb{E}_{q(x_1|x_0)}[\log p_\theta(x_0|x_1)] - \mathbb{E}_{q(x_{T-1}|x_0)}[D_{KL}(q(x_T|x_{T-1})||p(x_T))] \\ &\qquad \qquad - \sum_{t=1}^{T-1} \mathbb{E}_{q(x_{t-1},x_{t+1}|x_0)}[D_{KL}(q(x_t|x_{t-1})||p_\theta(x_t|x_{t+1}))] \end{align*}$$

• 第一项：reconstruction term，表示从第一层latent恢复原图的似然大小
• 第二项：prior matching term，当$x_T$为高斯时最小（取T足够大，$x_T$一定是高斯的，该项为0）
• 第三项：consistency term，努力使$x_t$处的前向、后向分布保持一致，当$p_\theta(x_t|x_{t+1})$训练至匹配高斯分布 $q(x_t|x_{t-1})$时，该项最小

第三项是优化的主要部分

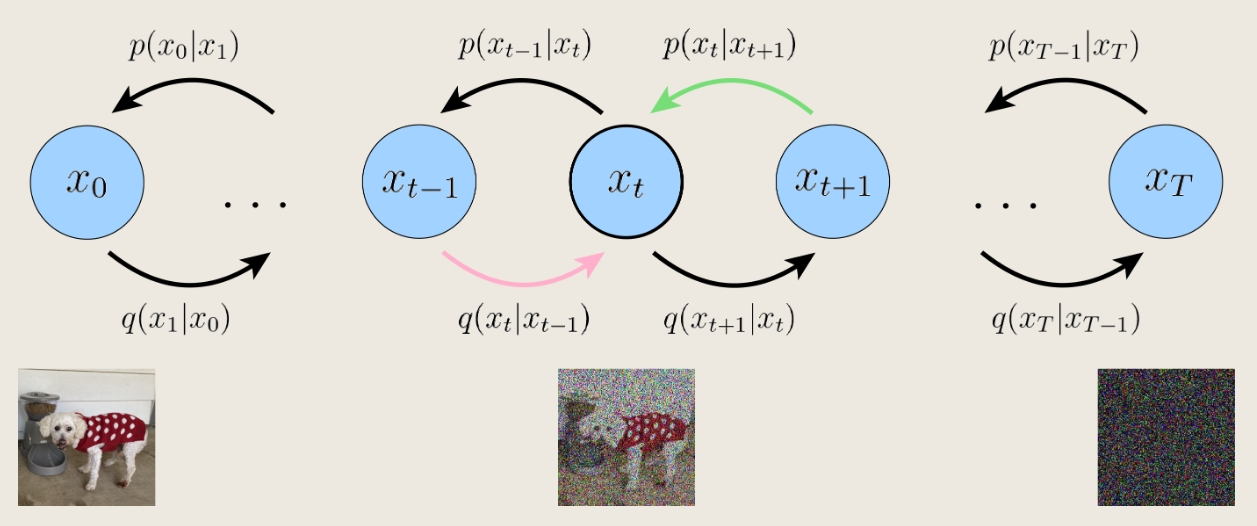
问题：第三项求期望用到了两个随机变量$x_{t-1}$和$x_{t+1}$，用Monte Carlo法结果方差较大

解决：利用$q(x_t|x_{t-1})=q(x_t|x_{t-1},x_0)=\frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}$重写ELBO项：

$$\begin{align*} \log p_\theta(x_0) &\ge \mathbb{E}_{q(x_{1:T}|x_0)}[\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}] = ELBO\\ &= \mathbb{E}_{q(x_1|x_0)}[\log p_\theta(x_0|x_1)] - D_{KL}(q(x_T|x_0)||p(x_T)) \\ &\qquad \qquad - \sum_{t=2}^{T} \mathbb{E}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))] \end{align*}$$

• 第一项：reconstruction term，表示从第一层latent恢复原图的似然大小
• 第二项：prior matching term，取T足够大，$x_T$几乎是纯高斯噪声，该项为0（能够用reparameterization trick证明$q(x_T|x_0)$是高斯的）
• 第三项：denoising matching term，衡量学习到的去噪过程与“真值”去噪过程的差异
  • 为什么不直接用“真值”去噪过程呢？——因为反向过程中$x_0$未知！

上述两个等式适用于任意MHVAE

第三项是优化的主要部分，其中$q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}$，其中：

• $q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf{I})$

• 在加噪过程的高斯过渡条件下，$q(x_{t-1}|x_0)$与$q(x_t|x_0)$可被计算：

  • $x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\epsilon\quad with \ \epsilon\sim\mathcal{N}(\epsilon;\mathbf{0},\mathbf{I})$
  • $x_{t-1}=\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon\quad with \ \epsilon\sim\mathcal{N}(\epsilon;\mathbf{0},\mathbf{I})$
  • …
  • $$\begin{align*} x_t &= \sqrt{\prod_{i=1}^{t}\alpha_i}x_0+\sqrt{1-\prod_{i=1}^{t}\alpha_i}\epsilon_0 \\ &= \sqrt{\bar{\alpha}}_tx_0+\sqrt{1-\bar{\alpha}_t}\epsilon_0 \\ &\sim \mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\mathbf{I}) \\ &= q(x_t|x_0) \end{align*}$$

因此：

$$\begin{align*} q(x_{t-1}|x_t,x_0) &= \frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &= \frac{\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf{I})\cdot\mathcal{N}(x_{t-1};\sqrt{\bar{\alpha}_{t-1}}x_0,(1-\bar{\alpha}_{t-1})\mathbf{I})}{\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\mathbf{I})} \\ &\propto \mathcal{N}(x_{t-1};\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t+\sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha}_t},\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{I}) \\ &= \mathcal{N}(x_{t-1};\mu_q(x_t,x_0),\Sigma_q(t)) \\ &= \mathcal{N}(x_{t-1};\mu_q(x_t,x_0),\sigma_q^2(t)\mathbf{I}) \end{align*}$$

综上：

$$\begin{align*} q(x_t|x_{t-1},x_0)&=q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathbf{I})\\q(x_{t-1}|x_t,x_0) &=\mathcal{N}(x_{t-1};\mu_q(x_t,x_0),\sigma_q^2(t)\mathbf{I})\\ &= \mathcal{N}(x_{t-1};\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t+\sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha}_t},\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{I}) \end{align*}$$

即前向过程的后验概率$x_{t-1}\sim q(x_{t-1}|x_t,x_0)$是高斯分布的
因此，把估计去噪过程$p_\theta(x_{t-1}|x_t)$建模为高斯的，且：

• 方差仍为$\Sigma_q(t)=\sigma_q^2(t)\mathbf{I}$，是“确定”的
• 均值建模为$\mu_\theta(x_t,t)$，不能与$x_0$有关！

为了使$p_\theta(x_{t-1}|x_t)$接近$q(x_{t-1}|x_t,x_0)$，等价于寻找参数$\theta$使得$\mu_\theta(x_t,t)$接近$\mu_q(x_t,x_0)$
将两者重写成如下形式：

$$\mu_q(x_t,x_0)=\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t+\sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha}_t}$$ $$\mu_\theta(x_t,t)=\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t+\sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)\hat{x}_\theta(x_t,t)}{1-\bar{\alpha}_t}$$

其中，$\mu_\theta(x_t,t)$的形式是“凑”出来的，为了与$\mu_q(x_t,x_0)$一致
$\hat{x}_\theta(x_t,t)$：用一个神经网络对$x_t$进行预测的结果，想要接近$x_0$

最优化问题变为：

$$\begin{align*} &\; \; \; \; \ \underset{\theta}{arg\ min}\ D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) \\ &= \underset{\theta}{arg\ min}\ \frac{1}{2\sigma_q^2(t)}[||\mu_\theta-\mu_q||_2^2] \\ &= \underset{\theta}{arg\ min}\ \frac{1}{2\sigma_q^2(t)}\frac{\bar{\alpha}_{t-1}(1-\alpha_t)^2}{(1-\bar{\alpha}_t)^2}[||\hat{x}_\theta(x_t,t)-x_0||_2^2] \end{align*}$$

且优化求和项$\sum_{t=2}^{T} \mathbb{E}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))]$近似于优化所有时间步长的期望：

$$\mathbb{E}_{t\sim U\{2,T\}}[\mathbb{E}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))]]$$

Learning Diffusion Noise Parameters

由于$SNR(t)=\frac{\mu(t)^2}{\sigma(t)^2}=\frac{\bar{\alpha}_t}{1-\bar{\alpha}_t}$，有：

$\frac{1}{2\sigma_q^2(t)}\frac{\bar{\alpha}_{t-1}(1-\alpha_t)^2}{(1-\bar{\alpha}_t)^2}[||\hat{x}_\theta(x_t,t)-x_0||_2^2]=\frac{1}{2}(SNR(t-1)-SNR(t))[||\hat{x}_\theta(x_t,t)-x_0||_2^2]$

$SNR(t)$需要随时间单调递减，可以用神经网络学习$SNR(t)$，设$SNR(t)=exp(-\omega_\eta(t))$，其中$\omega_\eta(t)$含参数$\eta$，随时间单调递增，有：

$\frac{\bar{\alpha}_t}{1-\bar{\alpha}_t}=exp(-\omega_\eta(t))$，$\bar{\alpha}_t=sigmoid(-\omega_\eta(t))$

优化目标需要同时对$\theta$、$\eta$进行优化

Three Equivalent Interpretations

等价于预测噪声

由$x_t$的重参数化式子可得：$x_0=\frac{x_t-\sqrt{1-\bar{\alpha}_t}\epsilon_0}{\sqrt{\bar{\alpha}_t}}$，带入$\mu_q(x_t,x_0)$式子可得：

$$\mu_q(x_t,x_0)=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}\sqrt{\alpha_t}}\epsilon_0$$

将$\mu_\theta(x_t,t)$构造为：

$$\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}\sqrt{\alpha_t}}\hat{\epsilon}_\theta(x_t,t)$$

故最优化问题变为：

$$\begin{align*} &\; \; \; \; \ \underset{\theta}{arg\ min}\ D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) \\ &= \underset{\theta}{arg\ min}\ \frac{1}{2\sigma_q^2(t)}\frac{(1-\alpha_t)^2}{(1-\bar{\alpha}_t)\alpha_t}[||\hat{\epsilon}_\theta(x_t,t)-\epsilon_0||_2^2] \end{align*}$$

即用神经网络预测使$x_0$成为$x_t$的噪声$\epsilon_0\sim\mathcal{N}(\epsilon;\mathbf{0},\mathbf{I})$
实验发现预测噪声效果更好

等价于预测score function

Tweedie’s Formula：
对于高斯变量$z\sim\mathcal{N}(z;\mu_z,\Sigma_z)$，$\mathbb{E}[\mu_z|z]=z+\Sigma_z\nabla_z\log p(z)$

由于$q(x_t|x_0)\sim \mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\mathbf{I})$，故：
$\mathbb{E}[\mu_{x_t}|x_t]=x_t+(1-\bar{\alpha}_t)\nabla_{x_t}\log p(x_t)=\sqrt{\bar{\alpha}_t}x_0$，即$x_0=\frac{x_t+(1-\bar{\alpha}_t)\nabla_{x_t}\log p(x_t)}{\sqrt{\bar{\alpha}_t}}$，带入$\mu_q(x_t,x_0)$式子可得:

$$\mu_q(x_t,x_0)=\frac{1}{\sqrt{\alpha_t}}x_t+\frac{1-\alpha_t}{\sqrt{\alpha_t}}\nabla_{x_t}\log p(x_t)$$

将$\mu_\theta(x_t,t)$构造为：

$$\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}x_t+\frac{1-\alpha_t}{\sqrt{\alpha_t}}s_\theta(x_t,t)$$

故最优化问题变为：

$$\begin{align*} &\; \; \; \; \ \underset{\theta}{arg\ min}\ D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) \\ &= \underset{\theta}{arg\ min}\ \frac{1}{2\sigma_q^2(t)}\frac{(1-\alpha_t)^2}{\alpha_t}[||s_\theta(x_t,t)-\nabla_{x_t}\log p(x_t)||_2^2] \end{align*}$$

即用神经网络预测score function $\nabla_{x_t}\log p(x_t)$

预测噪声项与score function关系

综合以上两种方法：

$$x_0=\frac{x_t+(1-\bar{\alpha}_t)\nabla_{x_t}\log p(x_t)}{\sqrt{\bar{\alpha}_t}}=\frac{x_t-\sqrt{1-\bar{\alpha}_t}\epsilon_0}{\sqrt{\bar{\alpha}_t}}$$ $$\nabla_{x_t}\log p(x_t) = -\frac{1}{\sqrt{1-\bar{\alpha}_t}}\epsilon_0$$

Score-based Generative Models

用score-based的视角解释第三种形式的原理

考虑energy-based models：

任意灵活概率分布可以写为：$p_\theta(x)=\frac{1}{Z_\theta}e^{-f_\theta(x)}$，其中$f_\theta(x)$使参数化的能量函数，通过神经网络建模；$Z_\theta$确保概率分布积分为1

问题：$Z_\theta$涉及对$f_\theta(x)$的积分，难以计算

对上式两边同时取对数求微分：

$\nabla_x\log p_\theta(x)=\nabla_x\log(\frac{1}{Z_\theta}e^{-f_\theta(x)})=-\nabla_xf_\theta(x)\approx s_\theta(x)$

直接用神经网络建模$s_\theta(x)$，避免计算$Z_\theta$

最优化函数：Fisher Divergence（F-散度）

$\mathbb{E}_{p(x)}[||s_\theta(x)-\nabla\log p(x)||_2^2]$

缺点：需要知道score function的真值

解决：score matching

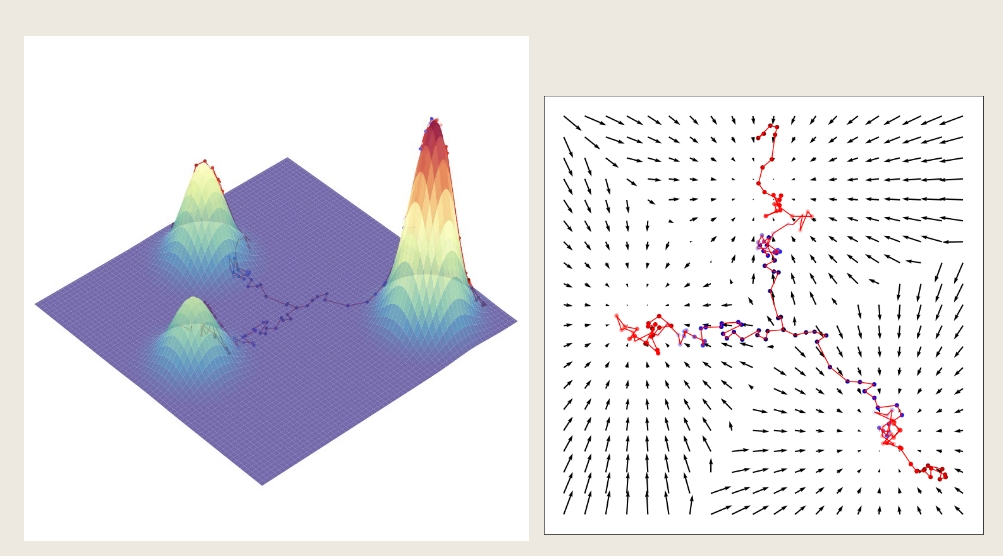
如图，score function表示了该如何移动来达到 $\log p(x)$的最大值

这被称作Langevin dynamics

$$x_{i+1}\gets x_i + c\nabla\log p(x_i) + \sqrt{2c}\epsilon, \qquad i=0,1,...,K$$

总的来说，学习过程将概率分布表示为分数函数，并使用它通过马尔科夫链蒙特卡罗技术（例如朗之万动力学）生成样本，称为基于分数的生成建模

score matching的问题：

• 当x位于高维空间中低维流形上时，score function的定义是病态的
• 训练出的score matching在低概率密度区域不准确
• 忽略掉了权重（混合系数）的影响

解决：向数据添加多层高斯噪音

• 首先，由于高斯噪音分布的支持是整个空间，因此受扰动的数据样本将不再局限于低维流形
• 其次，添加大的高斯噪音将增加每个模式在数据分布中覆盖的面积，从而在低密度区域添加更多的训练信号
• 最后，随着方差的增加，添加多个级别的高斯噪音将产生符合真值混合系数的中间分布

我们可以选择噪音水平的正序列$\{\sigma_t\}_{t=1}^T$，并定义逐渐扰动的数据分布序列，然后使用分数匹配学习神经网络$s_\theta(x,t)$，以同时学习所有噪音水平的分数函数

因此，我们在变分扩散模型和基于分数的生成模型之间建立了明确的联系

Guidance

上述只是学习$p(x)$，有时我们对学习$p(x|y)$感兴趣，这就是超分辨率、文生图等模型的基础
其中$y$可以是用来文生图的文字、用来超分辨的低分辨率图像等
此时，$p(x_{0:T})=p(x_T)\prod_{t=1}^{T}p_\theta(x_{t-1}|x_t)$变为$p(x_{0:T}|y)=p(x_T)\prod_{t=1}^{T}p_\theta(x_{t-1}|x_t,y)$

问题：训练过程中模型可能会淡化给定的条件信息
解决：提供guidance使模型给予条件信息足够的权重

• classifier guidance
• classifier-free guidance

代价：sample diversity（因为即使在噪音水平下，它也只会产生易于重新生成所提供的
条件信息的数据）

Classifier Guidance

$\nabla_{x_t}\log p(x_t|y) = \nabla_{x_t}\log(\frac{p(x_t)p(y|x_t)}{p(y)})=\nabla_{x_t}\log p(x_t)+\nabla_{x_t}\log p(y|x_t)$
第一项：无条件扩散模型的分数，按照之前推导的方式学习
第二项：接受任意有噪的$x_t$并尝试预测条件信息y的分类器的对抗梯度

加入超参数$\gamma$来控制模型考虑条件信息的比重后：

$$\nabla_{x_t}\log p(x_t|y)=\nabla_{x_t}\log p(x_t)+\gamma\nabla_{x_t}\log p(y|x_t)$$

缺点：依赖于一个独立的分类器，这个分类器可能需要被临时训练

Classifier-Free Guidance

由于$\nabla_{x_t}\log p(x_t|y)=\nabla_{x_t}\log p(x_t)+\nabla_{x_t}\log p(y|x_t)$，故：
$\nabla_{x_t}\log p(y|x_t)= - \nabla_{x_t}\log p(x_t)+\nabla_{x_t}\log p(x_t|y)$
代入上上式得：$\nabla_{x_t}\log p(x_t|y)=\gamma\nabla_{x_t}\log p(x_t|y)+(1-\gamma)\nabla_{x_t}\log p(x_t)$

由于学习两个单独的扩散模型的成本很高，因此我们可以将条件和无条件扩散模型作为单个条件模型一起学习；可以通过用固定的常数值（例如零）替换条件信息来查询无条件扩散模型。这本质上是对条件信息执行随机丢弃。